题目内容
已知函数f(x)=x3-3x
(1)试求函数y=f(x)的零点.
(2)求证:函数f(x)=x3-3x在[1,+∞)上是增函数.
(1)试求函数y=f(x)的零点.
(2)求证:函数f(x)=x3-3x在[1,+∞)上是增函数.
考点:函数零点的判定定理,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)直接求解方程x3-3x=0的根得函数y=f(x)的零点;
(2)求出函数f(x)的导函数,判断导函数在[1,+∞)上的符号得答案.
(2)求出函数f(x)的导函数,判断导函数在[1,+∞)上的符号得答案.
解答:
(1)解:由x3-3x=0,解得x1=0,x2=-
,x3=
.
∴函数y=f(x)的零点是0,-
,
;
(2)证明:∵f(x)=x3-3x,
∴f′(x)=3x2-3=3(x2-1),
∵x>1,
∴f′=3x2-3=3(x2-1)>0,
∴f(x)=x3-3x在[1,+∞)上是增函数.
| 3 |
| 3 |
∴函数y=f(x)的零点是0,-
| 3 |
| 3 |
(2)证明:∵f(x)=x3-3x,
∴f′(x)=3x2-3=3(x2-1),
∵x>1,
∴f′=3x2-3=3(x2-1)>0,
∴f(x)=x3-3x在[1,+∞)上是增函数.
点评:本题考查了函数零点的求法,考查了利用导数研究函数的单调性,是基础题.

练习册系列答案
相关题目
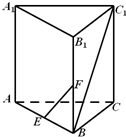 如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC,∠ABC=90°,点E,F分别是棱AB,BB1的中点,则直线EF和BC1所成的角是( )
如图,在直三棱柱ABC-A1B1C1中,AA1=AB=BC,∠ABC=90°,点E,F分别是棱AB,BB1的中点,则直线EF和BC1所成的角是( )| A、45° | B、135° |
| C、60° | D、120° |