题目内容
1.数列{an}中,a1=0,且对任意k∈N*,a2k-1,a2k,a2k+1成等差数列,其公差为2k,则Tn=$\frac{{2}^{2}}{{a}_{2}}+\frac{{3}^{2}}{{a}_{3}}+$…+$\frac{4{n}^{2}}{{a}_{2n}}$=4n-$\frac{3}{2}$-$\frac{1}{2n}$.分析 a1=0,且对任意k∈N*,a2k-1,a2k,a2k+1成等差数列,其公差为2k,可得a2k+1-a2k-1=4k,于是a2k-1=a1+(a3-a1)+(a5-a3)+…+(a2k-1-a2k-3)=2k(k-1),a2k=a2k-1+2k=2k2.即可得出.
解答 解:∵a1=0,且对任意k∈N*,a2k-1,a2k,a2k+1成等差数列,其公差为2k,
∴a2k+1-a2k-1=4k,
∴a2k-1=a1+(a3-a1)+(a5-a3)+…+(a2k-1-a2k-3)
=0+4+8+…+4(k-1)
=$\frac{k(0+4k-4)}{2}$=2k(k-1),
a2k=a2k-1+2k=2k2.
∴an=$\left\{\begin{array}{l}{\frac{{n}^{2}-1}{2},n=2k-1}\\{\frac{{n}^{2}}{2},n=2k}\end{array}\right.$(k∈N*).
当n=2k+1时,$\frac{{n}^{2}}{{a}_{n}}$=$\frac{2{n}^{2}}{{n}^{2}-1}$=2+$(\frac{1}{n-1}-\frac{1}{n+1})$,
当n=2k时,$\frac{{n}^{2}}{{a}_{n}}$=2.
∴Tn=$\frac{{2}^{2}}{{a}_{2}}+\frac{{3}^{2}}{{a}_{3}}+$…+$\frac{4{n}^{2}}{{a}_{2n}}$=2n+2(n-1)+$(\frac{1}{2}-\frac{1}{4})$+$(\frac{1}{4}-\frac{1}{6})$+…+$(\frac{1}{2n-2}-\frac{1}{2n})$
=4n-$\frac{3}{2}$-$\frac{1}{2n}$.
故答案为:4n-$\frac{3}{2}$-$\frac{1}{2n}$.
点评 本题考查了等差数列的通项公式及其前n项和公式、“裂项求和”,考查了分类讨论方法、推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案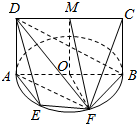 如图所示,矩形ABCD所在的平面垂直圆O所在的平面,AB是圆O的直径,M是CD上一点,且DM=EF,E、F是圆O上的点,∠EAF=∠FAB=30°.
如图所示,矩形ABCD所在的平面垂直圆O所在的平面,AB是圆O的直径,M是CD上一点,且DM=EF,E、F是圆O上的点,∠EAF=∠FAB=30°.