题目内容
已知a>0,函数f(x)=x|x-a|(x∈R).
(1)当a=2时,画出函数y=f(x)的大致图象;
(2)当a=2时,根据图象写出函数y=f(x)的单调减区间,并用定义证明你的结论;
(3)试讨论关于x的方程f(x)+1=a解的个数.
(1)当a=2时,画出函数y=f(x)的大致图象;

(2)当a=2时,根据图象写出函数y=f(x)的单调减区间,并用定义证明你的结论;
(3)试讨论关于x的方程f(x)+1=a解的个数.
考点:分段函数的应用
专题:综合题,函数的性质及应用
分析:(1)化简函数,结合二次函数的图象,可得结论;
(2)根据图象可写出函数y=f(x)的单调减区间,用定义证明时,先取值,再作差,定号,下结论即可;
(3)关于x的方程f(x)+1=a解的个数等价于y=f(x)与直线y=a-1的图象的交点个数.结合函数图象关于x的方程f(x)+1=a解的个数.
(2)根据图象可写出函数y=f(x)的单调减区间,用定义证明时,先取值,再作差,定号,下结论即可;
(3)关于x的方程f(x)+1=a解的个数等价于y=f(x)与直线y=a-1的图象的交点个数.结合函数图象关于x的方程f(x)+1=a解的个数.
解答:
解:(1)当a=2时,函数y=f(x)=
的大致图象如图所示;
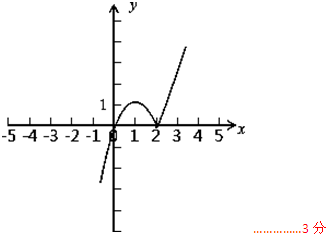
(2)当a=2时,f(x)=x|x-2|的单调递减区间是[1,2].
证明:设x1,x2∈[1,2],x1<x2,则f(x1)-f(x2)=(2x1-x12)-(2x2-x22)=(x1-x2)[2-(x1+x2)]
∵x1,x2∈[1,2],x1<x2,
∴x1-x2<0,2<x1+x2<4,
∴(x1-x2)[2-(x1+x2)]>0,
∴f(x1)>f(x2),
∴f(x)=x|x-2|的单调递减区间是[1,2].(8分)
(3)由题意,关于x的方程f(x)+1=a解的个数等价于y=f(x)与直线y=a-1的图象的交点个数.
∵f(
)=
,注意到f(
)-(a-1)=
(a-2)2≥0,当且仅当a=2时,等号成立.
∴根据图象可得,当0<a<1时,y=f(x)与直线y=a-1的图象有1个交点;
当a=1,a=2时,y=f(x)与直线y=a-1的图象有2个交点;
当1<a<2或a>2时,y=f(x)与直线y=a-1的图象有3个交点.(12分)
|
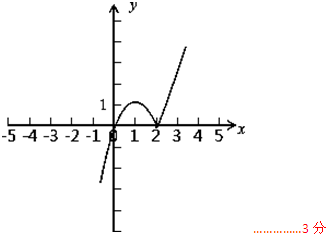
(2)当a=2时,f(x)=x|x-2|的单调递减区间是[1,2].
证明:设x1,x2∈[1,2],x1<x2,则f(x1)-f(x2)=(2x1-x12)-(2x2-x22)=(x1-x2)[2-(x1+x2)]
∵x1,x2∈[1,2],x1<x2,
∴x1-x2<0,2<x1+x2<4,
∴(x1-x2)[2-(x1+x2)]>0,
∴f(x1)>f(x2),
∴f(x)=x|x-2|的单调递减区间是[1,2].(8分)
(3)由题意,关于x的方程f(x)+1=a解的个数等价于y=f(x)与直线y=a-1的图象的交点个数.
∵f(
| a |
| 2 |
| a2 |
| 4 |
| a |
| 2 |
| 1 |
| 4 |
∴根据图象可得,当0<a<1时,y=f(x)与直线y=a-1的图象有1个交点;
当a=1,a=2时,y=f(x)与直线y=a-1的图象有2个交点;
当1<a<2或a>2时,y=f(x)与直线y=a-1的图象有3个交点.(12分)
点评:本题考查分段函数,考查函数的单调性,考查方程解的个数的讨论,考查数形结合的数学思想,属于中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
已知集合A={2,0,1,4},集合B={x|0<x≤4,x∈R},集合C=A∩B.则集合C可表示为( )
| A、{2,0,1,4} |
| B、{1,2,3,4} |
| C、{1,2,4} |
| D、{x|0<x≤4,x∈R} |
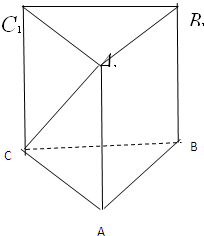 如图三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°,
如图三棱柱ABC-A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°,