题目内容

12．抛物线y2=2px（p＞0）的焦点为圆x2+y2-6x=0的圆心，过圆心且斜率为2的直线l与抛物线相交于M，N两点，则|MN|=（　　）
A．30B．25C．20D．15

分析 求出抛物线方程，直线l的方程为：y=x-1，与抛物线方程联立化为：y2+6y+1=0，利用根与系数的关系、抛物线的定义即可得出．

解答 解：圆x2+y2-6x=0的圆心（3，0），焦点F（3，0），抛物线y2=12x，
设M（x1，y1），N（x2，y2）．
直线l的方程为：y=2x-6，
联立$\left\{\begin{array}{l}{{y}^{2}=12x}\\{y=2x-6}\end{array}\right.$，化为：x2+-9x+9=0，
∴x1+x2=9，
∴|MN|=x1+x2+p=9+6=15，
故选：D．

点评 本题考查了抛物线的定义标准方程及其性质、直线与抛物线相交弦长问题、一元二次方程的根与系数的关系，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
2．设集合A={1，2，3}，B={2，3}，则A∪B=（　　）
A．{2}B．{3}C．{2}D．{1，2，3}
3．已知向量$\overrightarrow{a}$与$\overrightarrow{b}$满足$\overrightarrow{a}$=（2，0），|$\overrightarrow{b}$|=1，若|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{7}$，则a与b的夹角是$\frac{π}{3}$．
20．如图，抛物线C：y2=2px的焦点为F，抛物线上一定点Q（1，2）．
（1）求抛物线C的方程及准线l的方程；
（2）过焦点F的直线（不经过Q点）与抛物线交于A，B两点，与准线l交于点M，记QA，QB，QM的斜率分别为k1，k2，k3，问是否存在常数λ，使得k1+k2=λk3成立？若存在λ，求出λ的值；若不存在，说明理由．
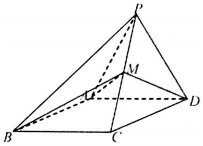7．如图所示，四棱锥P-ABCD的侧面PAD是边长为2的正三角形，底面ABCD是∠ABC=60°的菱形，M为PC的中点，PC=$\sqrt{6}$．
（Ⅰ）求证：PC⊥AD；
（Ⅱ）求三棱锥M-PAB的体积．
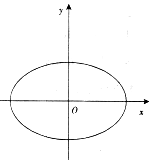17．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）和直线l：$\frac{x}{a}$-$\frac{y}{b}$=1，椭圆的离心率e=$\frac{\sqrt{6}}{3}$，坐标原点到直线l的距离为$\frac{\sqrt{3}}{2}$．
（Ⅰ）求椭圆的方程；
（Ⅱ）已知定点E（-1，0），若直线m过点P（0，2）且与椭圆相交于C，D两点，试判断是否存在直线m，使以CD为直径的圆过点E？若存在，求出直线m的方程；若不存在，请说明理由．
4．若命题p：α是第一象限角；命题q：α是锐角，则p是q的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
1．设x＞0，y＞0且x+4y=40，则lgx+lgy的最大值是（　　）
A．40B．10C．4D．2
2．已知函数f（x）=2cos（2x+$\frac{π}{3}$），函数g（x）的图象由函数f（x）的图象向右平移$\frac{π}{4}$个单位而得到，则当x∈[-$\frac{π}{2}$，$\frac{π}{2}$]时，g（x）的单调递增区间是[-$\frac{5π}{12}$，$\frac{π}{12}$]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网