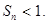题目内容
已知![]() .
.
(I)当![]() 时,解不等式
时,解不等式![]() ;
;
(II)当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(1)不等式的解集为![]() (2)
(2)![]()
解析:
(I)![]() 时,
时,![]() ,即
,即![]() (※)
(※)
(1)当![]() 时,由(※)
时,由(※)![]()
又![]() ,
,![]()
(2)当![]() 时,由(※)
时,由(※)![]()
又![]() ,
,![]()
(3)当![]() 时,由(※)
时,由(※)![]()
又![]() ,
,![]()
综上:由(1)、(2)、(3)知原不等式的解集为![]()
(II)当![]() 时,
时,![]() ,即
,即![]() 恒成立,
恒成立,
也即![]() 在
在![]() 上恒成立。
上恒成立。
而![]() 在
在![]() 上为增函数,故
上为增函数,故![]()
![]() 当且仅当
当且仅当![]() 即
即![]() 时,等号成立.
时,等号成立.
故![]()

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目

 时,求不等式
时,求不等式 的解集;
的解集; 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围.
 时,求
时,求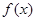 在[1,
在[1, ]上的取值范围。
]上的取值范围。 在[1,
在[1, .
. 时
时 取得极小值
取得极小值 ,求
,求 、
、 的值;
的值; 时,若在区间
时,若在区间 上至少存在一点
上至少存在一点 ,使得
,使得 成立,求实数
成立,求实数
 时,求函数
时,求函数 的单调区间;
的单调区间; ;
; 若
若 的前n项和,求证:
的前n项和,求证: