题目内容
已知函数![]()
(I)当![]() 时,求函数
时,求函数![]() 的极小值
的极小值
(II)试讨论曲线![]() 与
与![]() 轴的公共点的个数。
轴的公共点的个数。
(I)![]() 的极小值为
的极小值为![]()
(II)若![]()
![]() 的图象与
的图象与![]() 轴只有一个公共点;若
轴只有一个公共点;若![]() ,
,![]() 的图象与
的图象与![]() 轴有三个公共点。
轴有三个公共点。
解析:
(I)![]()
![]()
![]()
![]() 当
当![]() 或
或![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
![]() 在
在![]() ,(1,
,(1,![]() 内单调递增,在
内单调递增,在![]() 内单调递减
内单调递减
故![]() 的极小值为
的极小值为![]()
(II)①若![]() 则
则![]()
![]() 的图象与
的图象与![]() 轴只有一个交点。……6分
轴只有一个交点。……6分
②若![]() 则
则![]() ,
,![]() 当
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
![]() 的极大值为
的极大值为![]()
![]() 的极小值为
的极小值为![]()
![]() 的图象与
的图象与![]() 轴有三个公共点。
轴有三个公共点。
③若![]() ,则
,则![]() 。
。
![]() 当
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
![]() 的图象与
的图象与![]() 轴只有一个交点
轴只有一个交点
④若![]() ,则
,则![]()
![]() 的图象与
的图象与![]() 轴只有一个交点
轴只有一个交点
⑤当![]() ,由(I)知
,由(I)知![]() 的极大值为
的极大值为![]()
综上所述,若![]()
![]() 的图象与
的图象与![]() 轴只有一个公共点;
轴只有一个公共点;
若![]() ,
,![]() 的图象与
的图象与![]() 轴有三个公共点。
轴有三个公共点。

练习册系列答案
相关题目
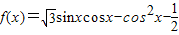
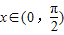 ,求f(x)的值域;
,求f(x)的值域;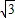 ,f(C)=0,若向量
,f(C)=0,若向量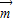 =(1,sinA)与向量
=(1,sinA)与向量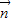 =(2,sinB)共线,求a,b的值.
=(2,sinB)共线,求a,b的值.
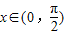 ,求f(x)的值域;
,求f(x)的值域; ,f(C)=0,若向量
,f(C)=0,若向量 =(1,sinA)与向量
=(1,sinA)与向量 =(2,sinB)共线,求a,b的值.
=(2,sinB)共线,求a,b的值.
 的单调区间;
的单调区间; 的最小值;
的最小值; ,使得
,使得 的取值范围.
的取值范围.
 的最小正周期及图象的对称轴方程式;
的最小正周期及图象的对称轴方程式; 的条件下,求
的条件下,求 的值.
的值.