题目内容
（本小题满分12分）
已知函数
（I）当
时，求函数
的单调区间；
（II）求证：
；
（III）已知数列
若
的前n项和，求证：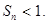
【答案】
（1）
函数
的增区间为
，减区间为
（2） 略
（3） 略
【解析】⑴解：函数的定义域为
，
, ……1分
当
时
，所以函数在上为增函数,
当
时
，所以函数在上为减函数,
故函数的增区间为，减区间为．……6分
⑵证明：由⑴得，当
时在
上是增函数,
所以
，即
．……8分
⑶证明：由⑵得
, …… 10分
．
即
成立． ………………………………………………12分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
