题目内容
已知函数 .
.
(I)当 时
时 取得极小值
取得极小值 ,求
,求 、
、 的值;
的值;
(II)当 时,若在区间
时,若在区间 上至少存在一点
上至少存在一点 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
【答案】
(1)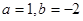 ;(2)(
;(2)(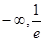 )
)
【解析】(I)根据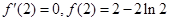 ,可建立关于a,b的两个方程,解方程组即可求出a,b的值.
,可建立关于a,b的两个方程,解方程组即可求出a,b的值.
(II)若在区间存在一点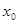 ,使得
,使得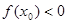 成立,转化为
成立,转化为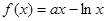 在区间
在区间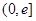 上的最小值小于0即可,然后利用导数求其最小值即可.
上的最小值小于0即可,然后利用导数求其最小值即可.
解:(I)求导数,得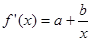 ……………2分
……………2分
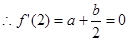 ①
①
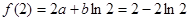 ②
②
由①②,解得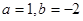 ……………4分
……………4分
此时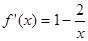
当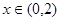 时,
时,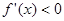 ;当
;当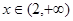 时
时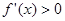
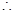 当
当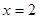 时
时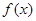 取得极小值
取得极小值
故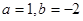 符合题目条件
…………………………………5分
符合题目条件
…………………………………5分
(II)当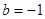 时,
时,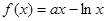 ,
,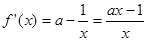
若在区间存在一点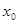 ,使得
,使得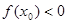 成立,只需
成立,只需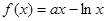 在
在
区间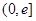 上的最小值小于0即可. ………………………………7分
上的最小值小于0即可. ………………………………7分
(1)当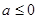 时,
时,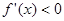 .函数
.函数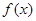 在
在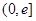 上单调递减,
上单调递减,
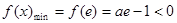 ,符合题意
……………………9分
,符合题意
……………………9分
(2)当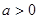 时,令
时,令 ,得
,得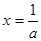
①若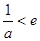 ,即
,即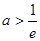 ,则
,则
|
|
(0, |
|
( |
|
|
- |
0 |
+ |
|
|
↘ |
极小值 |
↗ |
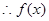 的极小值即最小值为
的极小值即最小值为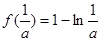
由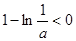 ,得
,得 ,不合题意
………………11分
,不合题意
………………11分
②若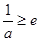 ,即
,即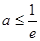 ,则
,则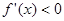 ,函数
,函数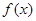 在
在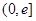
上单调递减
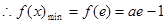
由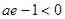 ,得
,得
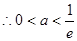 符合题意
……………………………………13分
符合题意
……………………………………13分
综上可知,实数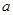 的取值范围为(
的取值范围为(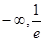 )
…………14分
)
…………14分

练习册系列答案
相关题目

 )
) )
)
 .
. .
. ,
, .
.