题目内容
【题目】设![]() 、
、![]() 为正整数,
为正整数,![]() 表示
表示![]() 的所有正约数的
的所有正约数的![]() 次方之和.证明:对于任意
次方之和.证明:对于任意![]() ,存在无穷多个正整数
,存在无穷多个正整数![]() ,使得
,使得![]() .
.
【答案】见解析
【解析】
通过递归构造数列![]() ,使得该正整数数列的每一项均符合要求,并且对任何正整数
,使得该正整数数列的每一项均符合要求,并且对任何正整数![]() ,均有
,均有![]() 严格整除
严格整除![]() .
.
先假设![]() 为
为![]() 的一个质因子.则
的一个质因子.则![]() 是奇数.
是奇数.
故![]() .
.
从而,![]() .
.
于是,![]() 满足要求.
满足要求.
其次假设![]() 已经取好.
已经取好.
接下来考虑![]() .
.
(1)若![]() 有一个质因子
有一个质因子![]() ,则
,则![]() .
.
所以,![]() 符合条件且被
符合条件且被![]() 严格整除,取
严格整除,取![]() 即可.
即可.
(2)若![]() 的质因子均是
的质因子均是![]() 的质因子,则
的质因子,则![]() 与
与![]() 的质因子标准分解式中的质数全部一样,设这两个标准分解式为
的质因子标准分解式中的质数全部一样,设这两个标准分解式为![]() ,
,![]() .
.
由于![]() (整体大于部分),故必存在某个
(整体大于部分),故必存在某个![]() .
.
不妨设![]() .则
.则![]() ,
,
且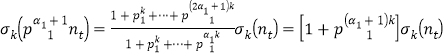
![]() .
.
因为![]() ,所以,
,所以,![]() 中含
中含![]() 的幂次大于或等于
的幂次大于或等于![]() .
.
从而,![]() .
.
因此,取![]() 符合要求.
符合要求.
由(1)、(2)及归纳原理,知可以构造出数列![]() .
.
从而,存在无穷多个![]() ,…满足要求.
,…满足要求.

练习册系列答案
相关题目