题目内容
【题目】甲、乙两人进行象棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,各局比赛结果相互独立.
,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)用X表示比赛决出胜负时的总局数,求随机变量X的分布列.
【答案】(1)![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】
用A表示“甲在4局以内(含4局)赢得比赛”,![]() 表示“第k局甲获胜”,
表示“第k局甲获胜”,![]() 表示“第k局乙获胜”则
表示“第k局乙获胜”则![]() ,
,![]() ,
,![]() .
.
(1)若甲在4局以内(含4局)赢得比赛分三类,一是前两局甲赢,二是第一局甲负,第二第三局赢,三是第一局甲赢,第二局甲负第三第四局甲赢.
(2)X的所有可能取值为![]() .然后分别求出相应的概率,列出分布列.
.然后分别求出相应的概率,列出分布列.
用A表示“甲在4局以内(含4局)赢得比赛”,![]() 表示“第k局甲获胜”,
表示“第k局甲获胜”,![]() 表示“第k局乙获胜”则
表示“第k局乙获胜”则![]() ,
,![]() ,
,![]() .
.
(1)![]()
![]()
![]() .
.
(2)X的所有可能取值为![]() .
.
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() .
.
∴X的分布列为
X | 2 | 3 | 4 | 5 |
P |
|
|
|
|

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
【题目】已知函数![]() 的定义域为[-1,5],部分对应值如下表,
的定义域为[-1,5],部分对应值如下表,![]() 的导函数
的导函数![]() 的图象如图所示,下列关于
的图象如图所示,下列关于![]() 的命题正确的是( )
的命题正确的是( )
|
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
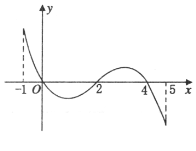
A.函数![]() 的极大值点为0,4;
的极大值点为0,4;
B.函数![]() 在[0,2]上是减函数;
在[0,2]上是减函数;
C.如果当![]() 时,
时,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最大值为4;
的最大值为4;
D.函数![]() 的零点个数可能为0、1、2、3、4个.
的零点个数可能为0、1、2、3、4个.