题目内容
已知三棱柱 的侧棱与底面垂直,体积为
的侧棱与底面垂直,体积为 ,底面是边长为
,底面是边长为 的正三角形.若
的正三角形.若 为底面
为底面 的中心,则
的中心,则 与平面
与平面 所成角的大小为( )
所成角的大小为( )
A. . . | B. | C. | D. |
B
解析试题分析:如图所示,∵ 底面
底面 ,∴
,∴ 为
为 与平面
与平面 所成角,∵平面
所成角,∵平面 ∥平面
∥平面 ,∴
,∴ 为
为 与平面
与平面 所成角,∵
所成角,∵ ,∴
,∴ ,解得
,解得 ,又
,又 为底面正三角形
为底面正三角形 的中心,∴
的中心,∴ 在
在 中,
中, ,∴
,∴ ,故选B.
,故选B.
考点:直线与平面所成的角.

练习册系列答案
相关题目
如果直线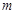 //直线
//直线 ,且
,且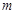 //平面
//平面 ,那么
,那么 与
与 的位置关系是( )
的位置关系是( )
| A.相交 | B. // // | C.   | D. // // 或 或   |
在空间中,过点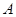 作平面
作平面 的垂线,垂足为
的垂线,垂足为 ,记
,记 .设
.设 是两个不同的平面,对空间任意一点
是两个不同的平面,对空间任意一点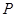 ,
, ,恒有
,恒有 ,则( )
,则( )
A.平面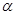 与平面 与平面 垂直 垂直 | B.平面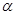 与平面 与平面 所成的(锐)二面角为 所成的(锐)二面角为 |
C.平面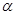 与平面 与平面 平行 平行 | D.平面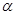 与平面 与平面 所成的(锐)二面角为 所成的(锐)二面角为 |
用斜二测画法作一个边长为2的正方形,则其直观图的面积为( )
A. | B. 2 | C.4 | D.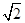 |
在正方体 中,
中, 是
是 的中点,则异面直线
的中点,则异面直线 与
与 所成角的大小是( )
所成角的大小是( )
A. | B. | C. | D. |





 ,CD=CB=
,CD=CB= ,且
,且 ,现将
,现将 沿着对角线BD翻折成
沿着对角线BD翻折成 ,则在
,则在 内的过程中,直线
内的过程中,直线 与平面
与平面

