题目内容
2.在平面几何里有射影定理:在△ABC中,AB⊥AC,点D是点A在BC边上的射影,则AC2=CD•CB.拓展到空间,在三棱锥A-BCD中,BA⊥平面ACD,点O是点A在平面BCD内的射影,类比平面三角形射影定理,得出${({{S_{△ACD}}})^2}$=S△DCO•S△BCD.分析 这是一个类比推理的题,在由平面图形到空间图形的类比推理中,一般是由点的性质类比推理到线的性质,由线的性质类比推理到面的性质,由已知在平面几何中在△ABC中,AB⊥AC,点D是点A在BC边上的射影,则AC2=CD•CB,我们可以类比这一性质,推理出若在三棱锥A-BCD中,BA⊥平面ACD,点O是点A在平面BCD内的射影,即可得到答案
解答 解:由已知在平面几何中,
在△ABC中,AB⊥AC,点D是点A在BC边上的射影,则AC2=CD•CB,
我们可以类比这一性质,推理出:
在三棱锥A-BCD中,BA⊥平面ACD,点O是点A在平面BCD内的射影,
则(S△ACD)2=S△DCO•S△BCD.
故答案为S△DCO•S△BCD
点评 类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
相关题目
12.在如图所示的算法流程图中,输出S的值为( )
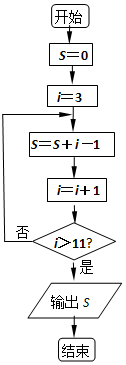

| A. | 51 | B. | 52 | C. | 53 | D. | 54 |
13.过点A(2,3)的直线的参数方程为$\left\{\begin{array}{l}{x=2+t}\\{y=3+2t}\end{array}\right.$(t为参数),若此直线与直线x-y+3=0相交于点B,则|AB|=( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | $\frac{3\sqrt{5}}{2}$ |
10.到一个三角形的三个顶点的距离的平方和最小的点,是这个三角形的( )
| A. | 垂心 | B. | 内心 | C. | 外心 | D. | 重心 |
17.两个分类变量X与Y有关系的可能性越大,随机变量K2的值( )
| A. | 越大 | B. | 越小 | ||
| C. | 不变 | D. | 可能越大也可能越小 |
7.设a>b,则下列不等式成立的是( )
| A. | a2>b2 | B. | $\sqrt{a}$>$\sqrt{b}$ | C. | 2a>2b | D. | lga>lgb |
14.设ab<0,则下列四个式子:(1)|a-b|=|a|+|b|,(2)|a-b|<|a+b|,(3)|a+b|<|b|,(4)|a-b|>|a|-|b|中,正确的是( )
| A. | (1)、(2) | B. | (1)、(4) | C. | (3)、(4) | D. | (2)、(4) |
11.在同一坐标系中,将曲线y=sinx通过φ:$\left\{\begin{array}{l}x'=2x\\ y'=3y\end{array}$变换后的曲线是( )
| A. | y'=3sin2x' | B. | y'=3sin$\frac{x'}{2}$ | C. | y'=$\frac{1}{3}$sin2x' | D. | y'=$\frac{1}{3}sin\frac{x'}{2}$ |
12. 某几何体的三视图如图所示,其中俯视图是半圆,则该几何体的体积为( )
某几何体的三视图如图所示,其中俯视图是半圆,则该几何体的体积为( )
 某几何体的三视图如图所示,其中俯视图是半圆,则该几何体的体积为( )
某几何体的三视图如图所示,其中俯视图是半圆,则该几何体的体积为( )| A. | $\frac{\sqrt{3}}{6}$π | B. | $\frac{3}{2}$π | C. | $\frac{1}{6}$π | D. | $\frac{\sqrt{3}}{3}$π |