题目内容
设f(x)=(sinx+cosx)ex+m,
(1)当m=0时,求f(x)在点(0,f(0))处的切线方程;
(2)若对于任意x∈[0,π],都有f(x)≥0,求m的取值范围.
(1)当m=0时,求f(x)在点(0,f(0))处的切线方程;
(2)若对于任意x∈[0,π],都有f(x)≥0,求m的取值范围.
解:(1)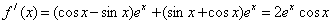 ,
,
则f(0)=1,f′(0)=2,
故f(x)在点(0,f(0))处的切线方程为y=2x+1。
(2)由(1)知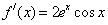 ,
,
由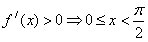 ;由
;由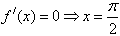 ;
;
由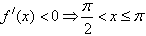 ,
,
故f(x)在区间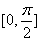 上为增函数,在区间
上为增函数,在区间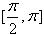 上为减函数,
上为减函数,
又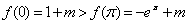 ,
,
故其最小值为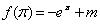 ,
,
要使f(x)≥0对任意实数x∈[0,π]恒成立,
只需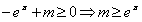 ,
,
即m的取值范围是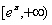 。
。
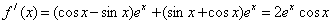 ,
,则f(0)=1,f′(0)=2,
故f(x)在点(0,f(0))处的切线方程为y=2x+1。
(2)由(1)知
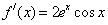 ,
,由
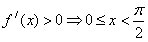 ;由
;由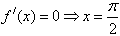 ;
;由
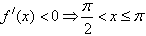 ,
,故f(x)在区间
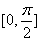 上为增函数,在区间
上为增函数,在区间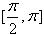 上为减函数,
上为减函数,又
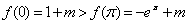 ,
,故其最小值为
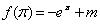 ,
,要使f(x)≥0对任意实数x∈[0,π]恒成立,
只需
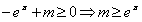 ,
,即m的取值范围是
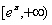 。
。 
练习册系列答案
相关题目