题目内容
6．已知函数f（x）=-$\frac{{x}^{2}+4x+7}{x+1}$，g（x）=lnx-$\frac{1}{2}$x2+$\frac{7}{2}$，实数a，b满足a＜b＜-1，若?x1∈[a，b]，?x2∈（0，+∞），使得f（x1）=g（x2）成立，则b-a的最大值为（ ）| A． | 2 | B． | 2$\sqrt{3}$ | C． | 2$\sqrt{2}$ | D． | 3 |
分析 求出g（x）max=g（1）=3，令t=x-1（t＜0），设h（t）=-2-（t-$\frac{4}{t}$），作函数y=f（t）的图象如图所示，由f（t）=3得t=-1或t=-4，即可得出结论．
解答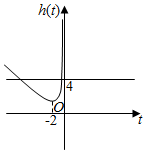 
解：∵g（x）=lnx-$\frac{1}{2}$x2+$\frac{7}{2}$，
∴g′（x）=$\frac{（1+x）（1-x）}{x}$，
∴0＜x＜1时＜X，g′（x）＞0；x＞1时，g′（x）＜0，
∴g（x）max=g（1）=3．
f（x）=-$\frac{{x}^{2}+4x+7}{x+1}$=-2+（-x-1-$\frac{4}{x+1}$），
令t=x+1（t＜0），设h（t）=-2+（-t-$\frac{4}{t}$），作函数y=h（t）的图象如图所示，
由f（t）=3得t=-1或t=-4，
∴b-a的最大值为3．
故答案为：3．
点评 本题考查导数知识的综合运用，考查函数的最大值，考查数形结合的数学思想，属于中档题．
练习册系列答案
相关题目
14．设a∈R，“cos2α=0”是“sinα=cosα”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
1．一个球与一个正三棱柱（底面是正三角形，侧棱垂直于底面的三棱柱）的三个侧面和两个底面都相切．已知这个球的体积是$\frac{9π}{2}$，那么这个三棱柱的体积是（ ）
| A． | 81$\sqrt{3}$ | B． | $\frac{81}{2}$$\sqrt{3}$ | C． | $\frac{81}{4}$$\sqrt{3}$ | D． | $\frac{81}{16}$$\sqrt{3}$ |