题目内容
18.若函数y1=x1lnx1,函数y2=x2-3,则(x1-x2)2+(y1-y2)2的最小值为2.分析 利用导数研究曲线的切线及其平行线之间的斜率关系、点到直线的距离公式即可得出.
解答 解:令f(x)=xlnx,g(x)=x-3,
f′(x)=lnx+1,令lnx0+1=1,解得x0=1.
∴可得y=x与曲线f(x)=xlnx相切于点P(1,0),与g(x)=x-3平行,
∴点P到直线g(x)=x-3的距离d的平方即为所求,
d=$\frac{|1-0-3|}{\sqrt{2}}$=$\sqrt{2}$,
∴(x1-x2)2+(y1-y2)2的最小值为2.
故答案为:2.
点评 本题考查了利用导数研究曲线的切线及其平行线之间的斜率关系、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.已知函数f(x)=-$\frac{{x}^{2}+4x+7}{x+1}$,g(x)=lnx-$\frac{1}{2}$x2+$\frac{7}{2}$,实数a,b满足a<b<-1,若?x1∈[a,b],?x2∈(0,+∞),使得f(x1)=g(x2)成立,则b-a的最大值为( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 3 |
10.i是虚数单位,若复数z满足zi=-1+i,则复数z的实部与虚部的和是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
8.盒子中共有12盒奶,工商人员从中任取3盒进行质量检查,则不同抽取方法的种数是( )
| A. | 22 | B. | 48 | C. | 84 | D. | 220 |
 如图,在△ABC中,∠ABC=90°,AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°.
如图,在△ABC中,∠ABC=90°,AB=2$\sqrt{3}$,BC=2,P为△ABC内一点,∠BPC=90°. 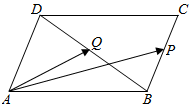 在边长为2的菱形ABCD中,∠BAD=60°,P,Q分别是BC,BD的中点,则向量$\overrightarrow{AP}$与$\overrightarrow{AQ}$的夹角的余弦值为$\frac{3\sqrt{21}}{14}$.
在边长为2的菱形ABCD中,∠BAD=60°,P,Q分别是BC,BD的中点,则向量$\overrightarrow{AP}$与$\overrightarrow{AQ}$的夹角的余弦值为$\frac{3\sqrt{21}}{14}$.