题目内容

17．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{3}（{x}^{3}+1），x≥0}\\{g（x）+3x，x＜0}\end{array}\right.$为奇函数，则g（-2）=4．

分析 由题意，f（-2）=-f（2），利用函数f（x）=$\left\{\begin{array}{l}{lo{g}_{3}（{x}^{3}+1），x≥0}\\{g（x）+3x，x＜0}\end{array}\right.$，即可得出结论．

解答 解：由题意，f（-2）=-f（2），
∴g（-2）-6=-log39，
∴g（-2）=4．
故答案为：4．

点评 本题考查函数的奇偶性，考查学生的计算能力，正确理解函数的奇偶性是关键．

练习册系列答案
相关题目
7．已知公差大于零的等差数列{an}满足：a3a4=48，a3+a4=14．
（Ⅰ） 求数列{an}通项公式；
（Ⅱ） 记${b_n}={（\sqrt{2}）^{a_n}}$，求数列{bn}的前n项和Tn．
8．已知函数f（x）=ax2+bx+c，当|x|≤1，|f（x）|≤1恒成立．若a=1，b=c，求实数b的取值范围．
5．若函数y=$\frac{3}{4}$x2-3x+4，x∈[a，b]总满足y∈[a，b]，则不等式（a+b）x＞-1的解集为（　　）
A．（-$\frac{1}{4}$，+∞）B．（-4，+∞）C．（-∞，-$\frac{1}{4}$）D．（-∞，-4）
12．已知数列{an}满足a1=1，an+1＞an，an+1+an-2$\sqrt{a{{\;}_{n}a}_{n+1}}$=1（n∈N*），求数列{an}的通项公式．
2．在数列{an}中，a1=1，（n+3）an+1=2nan（n∈N+），记bn=n（n+1）（n+2）an．
（1）求证：{bn}为等比数列；
（2）设cn=$\frac{{a}_{n}}{3•{2}^{n}}$，且数列{cn}的前n项和为Sn，求证：Sn＜$\frac{1}{4}$．
9．（1+x）3（1+y）4的展开式中x2y2的系数是18．
6．已知函数f（x）=-$\frac{{x}^{2}+4x+7}{x+1}$，g（x）=lnx-$\frac{1}{2}$x2+$\frac{7}{2}$，实数a，b满足a＜b＜-1，若?x1∈[a，b]，?x2∈（0，+∞），使得f（x1）=g（x2）成立，则b-a的最大值为（　　）
A．2B．2$\sqrt{3}$C．2$\sqrt{2}$D．3
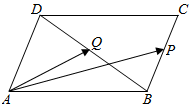7．在边长为2的菱形ABCD中，∠BAD=60°，P，Q分别是BC，BD的中点，则向量$\overrightarrow{AP}$与$\overrightarrow{AQ}$的夹角的余弦值为$\frac{3\sqrt{21}}{14}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网