题目内容
设{an}是首项为a1,公差为-1的等差数列,Sn为其前n项和,若S1,S2,S4成等比数列,则a1的值为 .
考点:等比数列的性质
专题:等差数列与等比数列
分析:由条件求得,Sn=
,再根据S1,S2,S4成等比数列,可得 S22=S1•S4,由此求得a1的值.
| n(2a1+1-n) |
| 2 |
解答:
解:由题意可得,an=a1+(n-1)(-1)=a1+1-n,Sn=
=
,
再根据若S1,S2,S4成等比数列,可得 S22=S1•S4,即 (2a1-1)2=a1•(4a1-6),
解得 a1=-
,
故答案为:-
.
| n(a1+an) |
| 2 |
| n(2a1+1-n) |
| 2 |
再根据若S1,S2,S4成等比数列,可得 S22=S1•S4,即 (2a1-1)2=a1•(4a1-6),
解得 a1=-
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题主要考查等差数列的前n项和公式,等比数列的定义和性质,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
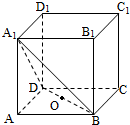 如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点,设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )
如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点,设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sinα的取值范围是( )A、[
| ||||||||
B、[
| ||||||||
C、[
| ||||||||
D、[
|