题目内容
16．由①安梦怡是高二（21）班学生；②安梦怡是独生子女，③高二（21）班的学生都是独生子女，写一个“三段论”形式的推理，则大前提，小前提和结论分别为（ ）| A． | ②①③ | B． | ③①② | C． | ①②③ | D． | ②③① |
分析 由题意，根据三段论的形式“大前提，小前提，结论”直接写出答案即可
解答 解：用三段论的形式写出的演绎推理是：
大前提：③高二（21）班的学生都是独生子女，
小前提：①安梦怡是高二（21）班学生，
结论：②安梦怡是独生子女．
故选：B．
点评 本题考查演绎推理--三段论，解题的关键是理解三段论的形式，本题是基础概念考查题．
练习册系列答案
阅读快车系列答案
相关题目
7．下面是一段“三段论”推理过程：设函数f（x）的导数为f′（x）．若函数f（x）在区间（a，b）内无极值点，则f′（x）在区间（a，b）内无零点．因为f（x）=x3在（-1，1）内无极值点，所以f′（x）=3x2在（-1，1）内无零点．以上推理中（ ）
| A． | 大前提错误 | B． | 小前提错误 | C． | 结论正确 | D． | 推理形式错误 |
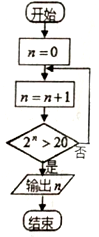
11．执行如图所示的程序框图，则输出的k为（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
1．已知△ABC中，A，B，C的对边分别是a，b，c，且2cos2$\frac{B}{2}=\sqrt{3}$sinB，a=3c
（Ⅰ）分别求tanC和sin2C的值；
（Ⅱ）若b=1，求△ABC的面积．
（Ⅰ）分别求tanC和sin2C的值；
（Ⅱ）若b=1，求△ABC的面积．
8．“a≥-3”是“xex+x2+ax+1＞0在（0，+∞）恒成立”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
6．
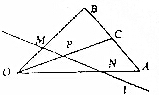如图，在△AOB中，OC是边AB的中线，P是OC的中点，直线l与OB，OA分别交于点M，N，若$\overrightarrow{OM}$=$\frac{3}{8}$$\overrightarrow{OB}$，$\overrightarrow{OA}$=x$\overrightarrow{ON}$，则x=（ ）
如图，在△AOB中，OC是边AB的中线，P是OC的中点，直线l与OB，OA分别交于点M，N，若$\overrightarrow{OM}$=$\frac{3}{8}$$\overrightarrow{OB}$，$\overrightarrow{OA}$=x$\overrightarrow{ON}$，则x=（ ）| A． | $\frac{5}{4}$ | B． | $\frac{4}{3}$ | C． | $\frac{3}{2}$ | D． | 2 |