题目内容
6.已知在数列{an}中,a1=a(0<a≤2),an+1=$\left\{\begin{array}{l}{{a}_{n}-2,{a}_{n}>2}\\{-{a}_{n}+3,{a}_{n}≤2}\end{array}\right.$(n∈N*),记Sn=a1+a2+…an.若Sn=2015,则n=1343.分析 a1=a(0<a≤2),an+1=$\left\{\begin{array}{l}{{a}_{n}-2,{a}_{n}>2}\\{-{a}_{n}+3,{a}_{n}≤2}\end{array}\right.$(n∈N*),可得a2=-a1+3=-a+3.分类讨论:当a∈(0,1)时,可得an+4=an.当a∈[1,2]时,可得:an+2=an.即可得出.
解答 解:∵a1=a(0<a≤2),an+1=$\left\{\begin{array}{l}{{a}_{n}-2,{a}_{n}>2}\\{-{a}_{n}+3,{a}_{n}≤2}\end{array}\right.$(n∈N*),
∴a2=-a1+3=-a+3.
①当a∈(0,1)时,3-a∈(2,3),∴a3=a2-2=1-a∈(0,1),∴a4=-a3+3=a+2∈(2,3),∴a5=a4-2=a∈(0,1),…,∴an+4=an.
∴a1+a2+a3+a4=a+(-a+3)+(1-a)+(a+2)=6.
∵Sn=2015=335×6+5,∴a1=a≠5,a1+a2=3≠5,a1+a2+a3=4-a≠5,舍去.
②当a∈[1,2]时,3-a∈[1,2],∴a3=-a2+3=a∈[1,2],∴an+2=an.
∵a1+a2=3,
∴Sn=2015=671×3+2,a1=a=2时,n=671×2+1=1343.
故答案为:1343.
点评 本题考查了递推关系、分类讨论方法、数列的周期性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
17.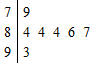 我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
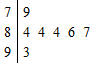 我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
我校为了丰富同学们的课余生活,特举办了一次挑战主持人大赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 4;4 | B. | 5;1.6 | C. | 84;4 | D. | 85;1.6 |
16.已知ω>0,|φ|<$\frac{π}{2}$,若x=$\frac{π}{6}$和x=$\frac{7π}{6}$是函数f(x)=cos(ωx+φ)的两个相邻的极值点,将y=f(x)的图象向左平移$\frac{π}{6}$个单位得到函数y=g(x)的图象,则下列说法正确的是( )
| A. | y=g(x)是奇函数 | B. | y=g(x)的图象关于点(-$\frac{π}{2}$,0)对称 | ||
| C. | y=g(x)的图象关于直线x=$\frac{π}{2}$对称 | D. | y=g(x)的周期为π |
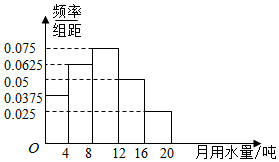 水是最常见的物质之一,是包括人类在内所有生命生存的重要资源,也是生物体最重要的组成部分,为了推动对水资源迸行综合性统筹规划和管理,加强水资源保护,解决日益严峻的淡水缺乏问题,开展广泛的宣传以提高公众对开发和保护水资源的认识,中国水利部确定每年的3月22日至28日为“中国水周”,以提倡市民节约用水.某市统计局凋查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如图所示.将月用水量落人各组的频率视为概率,并假设每天的用水量相互独立.
水是最常见的物质之一,是包括人类在内所有生命生存的重要资源,也是生物体最重要的组成部分,为了推动对水资源迸行综合性统筹规划和管理,加强水资源保护,解决日益严峻的淡水缺乏问题,开展广泛的宣传以提高公众对开发和保护水资源的认识,中国水利部确定每年的3月22日至28日为“中国水周”,以提倡市民节约用水.某市统计局凋查了该市众多家庭的用水量情况,绘制了月用水量的频率分布直方图,如图所示.将月用水量落人各组的频率视为概率,并假设每天的用水量相互独立.