题目内容
1．已知：（x+2）8=a0+a1（x+1）+a2（x+1）2+…+a8（x+1）8，其中ai=（i=0，1，2…8）为实常数，则a1+2a2+…+7a7+8a8=1024．分析 把所给的等式两边分别对x求导数，可得8（x+2）7=a1+2a2（x+1）+…+7a7（x+1）6+8a8（x+1）7，再令x=0，可得则a1+2a2+…+7a7+8a8的值．
解答 解：∵[1+（x+1）]8=a0+a1（x+1）+…+a8（x+1）8，其中ai=（i=0，1，2…8）为实常数，
两边分别对x求导数，可得8（x+2）7=a1+2a2（x+1）+…+7a7（x+1）6+8a8（x+1）7，
再令x=0，可得则a1+2a2+…+7a7+8a8=8•27=1024，
故答案为：1024．
点评 本题主要考查二项式定理的应用，求函数的导数，是给变量赋值的问题，关键是根据要求的结果，选择合适的数值代入，属于基础题．
练习册系列答案
相关题目
9．若函数y=$\frac{{2{{sin}^2}x+sin\frac{3x}{2}-4}}{{{{sin}^2}x+2{{cos}^2}x}}$既存在最大值M，又存在最小值m，则M+m的值为（ ）
| A． | -1 | B． | -2 | C． | -3 | D． | -4 |
16．已知ω＞0，|φ|＜$\frac{π}{2}$，若x=$\frac{π}{6}$和x=$\frac{7π}{6}$是函数f（x）=cos（ωx+φ）的两个相邻的极值点，将y=f（x）的图象向左平移$\frac{π}{6}$个单位得到函数y=g（x）的图象，则下列说法正确的是（ ）
| A． | y=g（x）是奇函数 | B． | y=g（x）的图象关于点（-$\frac{π}{2}$，0）对称 | ||
| C． | y=g（x）的图象关于直线x=$\frac{π}{2}$对称 | D． | y=g（x）的周期为π |
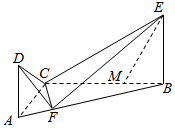如图，直角三角形ABC中，∠BAC=60°，点F在斜边AB上，且AB=4AF．D，E是平面ABC同一侧的两点，AD⊥平面ABC，BE⊥平面ABC，AD=3，AC=BE=4．
11．已知函数y=ax2+bx+c，其中a，b，c∈{0，1，2，3，4}，则不同的二次函数的个数共有（ ）
| A． | 125 | B． | 15 | C． | 100 | D． | 10 |