题目内容
20.已知△ABC的面积是$\frac{3-\sqrt{3}}{2}$,∠B为钝角,AB=2,BC=$\sqrt{3}$-1,则∠C的度数为450.分析 利用面积求出角B,再利用余弦定理求出AC,即可求出角C.
解答 解:由s=$\frac{1}{2}AB•AC•sinB$=$\frac{3-\sqrt{3}}{2}$,可得sinB=$\frac{\sqrt{3}}{2}$,
∵∠B为钝角,∴B=$\frac{2π}{3}$.
在△ABC中,由余弦定理得:AC2=AB2+CB2-2AB•CB•cosB,⇒AC=$\sqrt{6}$,
由正弦定理得$\frac{AB}{sinC}=\frac{AC}{sinB}$,解得sinC=$\frac{\sqrt{2}}{2}$,
∵C为锐角,∴C=45°.
故答案为:450
点评 本题考查了正余弦定理的应用,属于中档题.

练习册系列答案
相关题目
8.已知abcd≠0,则“a,b,c,d成等比数列”是“ad=bc”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
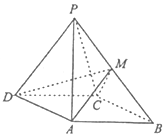 如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为2$\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.
如图,四棱锥P-ABCD中,侧面PDC是正三角形,底面ABCD是边长为2$\sqrt{3}$的菱形,∠DAB=120°,且侧面PDC与底面垂直,M为PB的中点.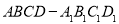 中,
中, 在线段
在线段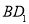 上,且
上,且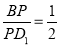 ,
,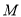 为线段
为线段 上的动点,则三棱锥
上的动点,则三棱锥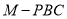 的体积为( )
的体积为( )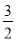
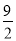 D.与
D.与 点的位置有关
点的位置有关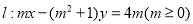 和圆
和圆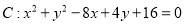 .有以下几个结论:
.有以下几个结论: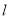 的倾斜角不是钝角;
的倾斜角不是钝角;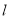 必过第一、三、四象限;
必过第一、三、四象限;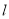 能将圆
能将圆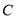 分割成弧长的比值为
分割成弧长的比值为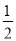 的两段圆弧;
的两段圆弧;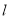 与圆
与圆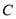 相交的最大弦长为
相交的最大弦长为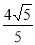 .
.