题目内容
12.已知各项均为正数的数列{an}满足an+2+2$\sqrt{{a}_{n}{a}_{n+2}}$=4an+1-an(n∈N*),且a1=1,a2=4.(1)证明:数列{$\sqrt{{a}_{n}}$}是等差数列;
(2)数列{$\frac{4n+2}{{a}_{n}{a}_{n+1}}$}的前项n和为Sn,求证:Sn<2.
分析 (1)通过关系式an+2+2$\sqrt{{a}_{n}{a}_{n+2}}$=4an+1-an(n∈N*)计算出前几项的值,猜想通项公式,进而利用数学归纳法证明即可;
(2)通过(1)裂项可知$\frac{4n+2}{{a}_{n}{a}_{n+1}}$=2[$\frac{1}{{n}^{2}}$-$\frac{1}{(n+1)^{2}}$],进而并项相加、放缩即得结论.
解答 证明:(1)依题意,a3+2$\sqrt{{a}_{3}}$=4×4-1,
整理得:($\sqrt{{a}_{3}}$-3)($\sqrt{{a}_{3}}$+5)=0,
解得:$\sqrt{{a}_{3}}$=3或$\sqrt{{a}_{3}}$=-5(舍),
又∵a4+2$\sqrt{4{a}_{4}}$=4×32-4,
∴a4+4$\sqrt{{a}_{4}}$-32=0,
解得:$\sqrt{{a}_{4}}$=4或$\sqrt{{a}_{4}}$=-8(舍),
猜想:$\sqrt{{a}_{n}}$=n.
下面用数学归纳法来证明:
①当n=1时,结论显然成立;
②假设当n=k时,有$\sqrt{{a}_{k}}$=k,
则ak+1+2$\sqrt{{a}_{k-1}•{a}_{k+1}}$=4ak-ak-1,
即ak+1+2(k-1)$\sqrt{{a}_{k+1}}$-3k2-2k+1=0,
整理得:[$\sqrt{{a}_{k+1}}$-(k+1)][$\sqrt{{a}_{k+1}}$+(3k-1)]=0,
解得:$\sqrt{{a}_{k+1}}$=k+1或$\sqrt{{a}_{k+1}}$=-3k+1(舍),
即当n=k+1时结论成立;
由①②可知,$\sqrt{{a}_{n}}$=n,
于是数列{$\sqrt{{a}_{n}}$}是首项、公差均为1的等差数列;
(2)由(1)可知an=n2,
则$\frac{4n+2}{{a}_{n}{a}_{n+1}}$=$\frac{4n+2}{{n}^{2}•(n+1)^{2}}$=2[$\frac{1}{{n}^{2}}$-$\frac{1}{(n+1)^{2}}$],
于是Sn=2[1-$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{2}}$-$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$-$\frac{1}{(n+1)^{2}}$]
=2[1-$\frac{1}{(n+1)^{2}}$]
<2.
点评 本题考查等差数列的证明及数列的前n项和的计算,考查数学归纳法,考查裂项相消法,注意解题方法的积累,属于中档题.

| A. | [-$\frac{1}{2}$,1] | B. | [-2,1] | C. | (-∞,-2]∪[1,+∞) | D. | (-∞,-$\frac{1}{2}$]∪[1,+∞) |
| A. | 6 | B. | 12 | C. | 32 | D. | 64 |
| A. | 2 | B. | 3 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
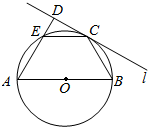 如图,AB是圆O的直径,C为圆周上一点,过C作圆O的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E.
如图,AB是圆O的直径,C为圆周上一点,过C作圆O的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E.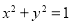 上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线
上每一点的纵坐标保持不变,横坐标变为原来的2倍得到曲线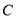 .
.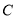 的参数方程;
的参数方程;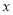 轴正半轴为极轴坐标建立极坐标系,已知直线
轴正半轴为极轴坐标建立极坐标系,已知直线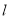 的极坐标方程为
的极坐标方程为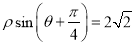 ,若
,若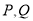 分别为曲线
分别为曲线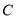 和直线
和直线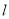 上的一点,求
上的一点,求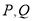 的最近距离.
的最近距离.