题目内容
16.在矩形ABCD中,将△ABC沿其对角线AC折起来得到△AB1C,且顶点B1在平面ACD上的射影O恰好落在边AD上(如图所示).(Ⅰ)证明:AB1⊥平面B1CD;
(Ⅱ)若AB=1,BC=$\sqrt{3}$,求三棱锥B1-ABC的体积.
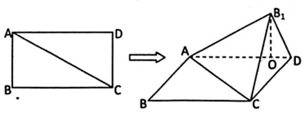
分析 (Ⅰ)利用线面垂直的判定证明AB1⊥CD,又AB1⊥B1C,且B1C∩CD=C,可得AB1⊥平面B1CD;
(Ⅱ)根据体积公式,由已知求得△ABC的面积,而高即为B1O,又易证△AB1D为直角△,则斜边AD上的高B1O可求,则三棱锥B1-ABC的体积可求.
解答 (Ⅰ)证明:如图,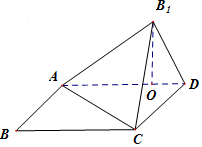
∵ABCD是矩形,∴AB⊥BC,则AB1⊥B1C,
在三棱锥B1-ACD中,∵B1O⊥面ACD,∴B1O⊥CD,
又CD⊥AD,且AD∩B1O=O,∴CD⊥平面AB1O,则CD⊥AB1,
又B1C∩CD=C,∴AB1⊥平面B1CD;
(Ⅱ)解:由于AB1⊥平面B1CD,B1D?平面ABCD,
∴AB1⊥B1D,在Rt△AB1D中,${B}_{1}D=\sqrt{A{D}^{2}-A{{B}_{1}}^{2}}=\sqrt{2}$,
又由B1O•AD=AB1•B1D,得${B}_{1}O=\frac{A{B}_{1}•{B}_{1}D}{AD}$=$\frac{\sqrt{6}}{3}$,
∴${V}_{{B}_{1}-ABC}=\frac{1}{3}$S△ABC•B1O=$\frac{1}{3}×\frac{1}{2}$×1×$\sqrt{3}$×$\frac{\sqrt{6}}{3}$=$\frac{\sqrt{2}}{6}$.
点评 本题考查线面垂直的判定,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
6.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,且F2为抛物线y2=24x的焦点,设点P为两曲线的一个公共点,若△PF1F2的面积为36$\sqrt{6}$,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{27}$=1 | B. | $\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{9}$=1 | C. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 | D. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 |
7.已知向量$\overrightarrow{a}$=(-2,4),$\overrightarrow{b}$=(-1,m).若$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数m的值为( )
| A. | -$\frac{1}{2}$ | B. | -2 | C. | 2 | D. | $\frac{1}{2}$ |
4.设集合M={-4,-3,-2,-1,0,1},N={x∈R|x2+3x<0},则M∩N=( )
| A. | {-3,-2,-1,0} | B. | {-2,-1,0} | C. | {-3,-2,-1} | D. | {-2,-1} |
11.已知实数x,y满足条件$\left\{\begin{array}{l}{x≤2}\\{x+y≥2}\\{2x-y≥2}\end{array}\right.$,则$\frac{y+x}{y+2x}$的取值范围是( )
| A. | [0,1] | B. | [$\frac{1}{3}$,1] | C. | [$\frac{1}{2}$,$\frac{2}{3}$] | D. | [$\frac{1}{2}$,1] |
8.随着国家二孩政策的全面放开,为了调查一线城市和非一线城市的二孩生育意愿,某机构用简单随机抽样方法从不同地区调查了100位育龄妇女,结果如表.
附表:
由K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$算得,K2=$\frac{100×(45×22-20×13)^{2}}{58×42×35×65}$≈9.616参照附表,得到的正确结论是( )
| 非一线 | 一线 | 总计 | |
| 愿生 | 45 | 20 | 65 |
| 不愿生 | 13 | 22 | 35 |
| 总计 | 58 | 42 | 100 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别有关” | |
| B. | 在犯错误的概率不超过0.1%的前提下,认为“生育意愿与城市级别无关” | |
| C. | 有99%以上的把握认为“生育意愿与城市级别有关” | |
| D. | 有99%以上的把握认为“生育意愿与城市级别无关” |
5.从1、2、3、4、5、6中任三个数,则所取的三个数按一定的顺序可排成等差数列的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{7}{20}$ |
6.已知直角梯形ABCD中,AB∥CD,AB⊥AD,AB=4,CD=6,AD=5,点E在梯形内,那么∠AEB为钝角的概率为( )
| A. | $\frac{2π}{25}$ | B. | $\frac{4π}{25}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |