题目内容
15.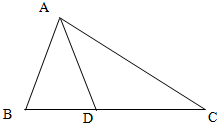 如图,在△ABC中,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow b$,点D在BC边上.
如图,在△ABC中,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow b$,点D在BC边上.( I)若D为BC边中点,求证:$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow a$+$\overrightarrow b$)
( II)若$\overrightarrow{AD}$=λ$\overrightarrow a$+μ$\overrightarrow b$,求证:λ+μ=1.
分析 (Ⅰ)根据图形,可以得到$\overrightarrow{BC}=\overrightarrow{b}-\overrightarrow{a}$,从而$\overrightarrow{BD}=\frac{1}{2}(\overrightarrow{b}-\overrightarrow{a})$,根据$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}$即可得出$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{a}+\overrightarrow{b})$;
(Ⅱ)根据点D在BC边上,便可得出存在t使得$\overrightarrow{BD}=t\overrightarrow{BC}=t(\overrightarrow{b}-\overrightarrow{a})$,进行向量的数乘运算即可求出$\overrightarrow{AD}=(1-t)\overrightarrow{a}+t\overrightarrow{b}$,根据平面向量基本定理即可得出$\left\{\begin{array}{l}{λ=1-t}\\{μ=t}\end{array}\right.$,从而得出λ+μ=1.
解答 证明:(I)∵$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$;
∴$\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow b-\overrightarrow a$;
又D为BC边中点,∴$\overrightarrow{BD}=\frac{1}{2}\overrightarrow{BC}=\frac{1}{2}(\overrightarrow b-\overrightarrow a)$;
∴$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{a+}\frac{1}{2}(\overrightarrow b-\overrightarrow a)=\frac{1}{2}(\overrightarrow a+\overrightarrow b)$;
(II)∵点D在BC边上,∴$\overrightarrow{BD}∥\overrightarrow{BC}$;
则存在实数t,使得$\overrightarrow{BD}=t\overrightarrow{BC}=t(\overrightarrow b-\overrightarrow a)$,
则$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow a+t(\overrightarrow b-\overrightarrow a)=(1-t)\overrightarrow a+t\overrightarrow b$;
若$\overrightarrow{AD}=λ\overrightarrow a+μ\overrightarrow b$,则λ=1-t,μ=t;
∴λ+μ=(1-t)+t=1.
点评 考查向量减法、减法及数乘的几何意义,以及向量的数乘运算,共线向量和平面向量基本定理.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案| A. | (-1,0) | B. | (-1,+∞) | C. | (0,+∞) | D. | (-∞,-1)∪(0,+∞) |