题目内容
10.已知直线l的参数方程为$\left\{\begin{array}{l}x=-t\\ y=-1+t\end{array}$(t为参数).以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=$\sqrt{2}$cos(θ+$\frac{π}{4}$).(Ⅰ)写出直线l的极坐标方程;
(Ⅱ)求直线l与曲线C交点的极坐标(ρ≥0,0≤θ<2π).
分析 (Ⅰ)由直线l的参数方程为$\left\{\begin{array}{l}x=-t\\ y=-1+t\end{array}\right.$(t为参数),消去参数t,得到直线l的普通方程,利用互化公式可得极坐标方程.
(Ⅱ)曲线C的极坐标方程为ρ=$\sqrt{2}$cos(θ+$\frac{π}{4}$),展开可得:$\frac{\sqrt{2}}{2}$ρ=$\sqrt{2}$(cosθ-sinθ).利用互化公式可得直角坐标方程,与直线方程联立即可得出交点坐标.
解答 解:(Ⅰ)∵直线l的参数方程为$\left\{\begin{array}{l}x=-t\\ y=-1+t\end{array}\right.$(t为参数),
∴消去参数t,得到直线l的普通方程x+y+1=0,
利用互化公式可得极坐标方程:ρcosθ+ρsinθ+1=0.
(Ⅱ)曲线C的极坐标方程为ρ=$\sqrt{2}$cos(θ+$\frac{π}{4}$),
展开可得:$\frac{\sqrt{2}}{2}$ρ=$\sqrt{2}$(cosθ-sinθ).
即ρ2=ρcosθ-ρsinθ,∴x2+y2=x-y.
联立方程$\left\{\begin{array}{l}x+y+1=0\\{x^2}+y{\;}^2=x-y\end{array}\right.$
∴解得l与C交点的直角坐标为:(0,-1),
极坐标为(1,$\frac{3π}{2}$).
点评 本题考查了直线的参数方程与极坐标方程、极坐标与直角坐标方程的互化公式、直线与圆的交点,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.设a∈R,若函数y=ex-2ax,x∈R有大于0的极值点,则( )
| A. | a<$\frac{1}{e}$ | B. | a>$\frac{1}{e}$ | C. | a>$\frac{1}{2}$ | D. | a<$\frac{1}{2}$ |
19.已知点A(1,1),B(5,3),向量$\overrightarrow{AB}$绕点A逆时针旋转$\frac{π}{2}$到$\overrightarrow{AC}$的位置,则点C的坐标为( )
| A. | (-1,5) | B. | (1,-5) | C. | (-4,2) | D. | (2,-4) |
20.在△ABC中,∠A=90°,AB=1,则$\overrightarrow{AB}$•$\overrightarrow{BC}$等于( )
| A. | 1 | B. | -1 | C. | 0 | D. | $\sqrt{2}$ |
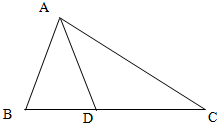 如图,在△ABC中,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow b$,点D在BC边上.
如图,在△ABC中,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow b$,点D在BC边上.