题目内容
5.设函数f(x)=lnx-$\frac{1}{2}$ax2-bx,若x=1是f(x)的极大值点,则a的取值范围为( )| A. | (-1,0) | B. | (-1,+∞) | C. | (0,+∞) | D. | (-∞,-1)∪(0,+∞) |
分析 求出函数的f(x)的定义域,f'(x),由f'(1)=0,得b=1-a,通过讨论a的范围,去掉函数的单调区间,结合已知条件求出a的取值范围即可.
解答 解:f(x)的定义域为(0,+∞),f'(x)=$\frac{1}{x}$-ax-b,由f'(1)=0,得b=1-a.
所以f'(x)=$\frac{-(ax+1)(x-1)}{x}$.
①若a≥0,由f'(x)=0,得x=1.
当0<x<1时,f'(x)>0,此时f(x)单调递增;
当x>1时,f'(x)<0,此时f(x)单调递减.
所以x=1是f(x)的极大值点.
②若a<0,由f'(x)=0,得x=1,或x=-$\frac{1}{a}$.
因为x=1是f(x)的极大值点,所以-$\frac{1}{a}$>1,解得-1<a<0.
综合①②:a的取值范围是a>-1.
故选:B.
点评 本题考查函数的单调性、极值等知识点的应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
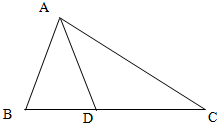 如图,在△ABC中,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow b$,点D在BC边上.
如图,在△ABC中,设$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow b$,点D在BC边上.