Question

6．三棱锥P-ABC中，$AB=AC=\sqrt{2}$，AP=BC=2，$BP=\sqrt{6}$，BC⊥AP，则此三棱锥的外接球的体积为（　　）

• A． $\frac{{4\sqrt{2}π}}{3}$
• B． $\frac{{8\sqrt{2}π}}{3}$
• C． $\frac{{16\sqrt{2}π}}{3}$
• D． $\frac{{32\sqrt{2}π}}{3}$

Answer 1

分析 根据勾股定理可判断AP⊥AB，AB⊥AC，AP⊥平面ABC，求出三棱锥的外接球的直径，即可求出三棱锥的外接球的体积．

解答 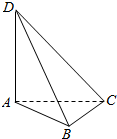解：∵AP=2，AB=$\sqrt{2}$，$BP=\sqrt{6}$，满足AP²+AB²=PB²
∴AP⊥AB，又AP⊥BC，BC∩AB=B，
∴AP⊥平面ABC，
∵AB=AC=$\sqrt{2}$，BC=2，∴AB⊥AC，
∴三棱锥的外接球的直径是$\sqrt{4+2+2}$=2$\sqrt{2}$，
∴三棱锥的外接球的体积为$\frac{4}{3}π•（\sqrt{2}）^{3}$=$\frac{8\sqrt{2}π}{3}$．
故选：B．

点评 本题考查了三棱锥的外接球的体积，关键是根据线段的数量关系求出三棱锥的外接球的直径．