题目内容
18.棱长为2的正方体ABCD-A1B1C1D1中,已知E,F在棱C1D1上运动,且EF=1,P为CC1的中点,若Q在AB上运动,则四面体QEFP的体积为$\frac{1}{6}$.分析 如图所示,连接BC1,过中点P作PM⊥BC1,垂足为M.利用正方体的性质与面面垂直的性质可得:PM⊥平面ABC1D1.PM=PC1sin45°.S△EFQ=$\frac{1}{2}EF•B{C}_{1}$.可得VP-EFQ=$\frac{1}{3}PM•{S}_{△EFQ}$.
解答 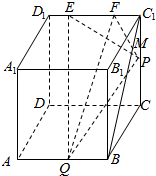 解:如图所示,
解:如图所示,
连接BC1,过中点P作PM⊥BC1,垂足为M.
由正方体的性质可得:平面ABC1D1⊥平面BCC1B1,
则PM⊥平面ABC1D1.
PM=PC1sin45°=$\frac{\sqrt{2}}{2}$.
S△EFQ=$\frac{1}{2}EF•B{C}_{1}$=$\frac{1}{2}×1×\sqrt{2}$.
∴VP-EFQ=$\frac{1}{3}PM•{S}_{△EFQ}$=$\frac{1}{3}×\frac{\sqrt{2}}{2}$×$\frac{\sqrt{2}}{2}$=$\frac{1}{6}$.
故答案为:$\frac{1}{6}$.
点评 本题考查了空间位置关系、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
6.三棱锥P-ABC中,$AB=AC=\sqrt{2}$,AP=BC=2,$BP=\sqrt{6}$,BC⊥AP,则此三棱锥的外接球的体积为( )
| A. | $\frac{{4\sqrt{2}π}}{3}$ | B. | $\frac{{8\sqrt{2}π}}{3}$ | C. | $\frac{{16\sqrt{2}π}}{3}$ | D. | $\frac{{32\sqrt{2}π}}{3}$ |
3.“x=1”是“x2-1=0”的( )
| A. | 充分必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分而不必要条件 | D. | 既不充分也不必要条件 |
8.在△ABC中,角A,B,C所对的边分别为a,b,c,若 c2-b2=$\sqrt{3}$ab,sinA=2$\sqrt{3}$sinB,则角C=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
 如图,在△ABC中,点D在BC边上,AD⊥AC,$cosB=\frac{{\sqrt{6}}}{3}$,$AB=3\sqrt{2}$,$BD=\sqrt{3}$.
如图,在△ABC中,点D在BC边上,AD⊥AC,$cosB=\frac{{\sqrt{6}}}{3}$,$AB=3\sqrt{2}$,$BD=\sqrt{3}$.