Question

6．已知圆C：（x-2）²+（y-1）²=1，点P为直线x+2y-9=0上一动点，过点P向圆C引两条切线PA，PB，其中A，B为切点，则$\overrightarrow{PA}•\overrightarrow{PB}$的取值范围为[$\frac{12}{5}$，+∞）．

Answer 1

分析 设∠APB=2θ，用θ表示出$\overrightarrow{PA}•\overrightarrow{PB}$，求出θ的范围即可得出$\overrightarrow{PA}•\overrightarrow{PB}$的范围．

解答 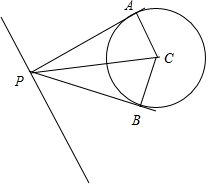解：设∠APB=2θ，则PA=PB=$\frac{1}{tanθ}$，
∴当CP取得最小值时，θ取得最大值．
圆心C（2，1）到直线x+2y-9=0的距离为$\frac{|2+2-9|}{\sqrt{5}}$=$\sqrt{5}$，圆的半径为r=1，
∴sinθ的最大值为$\frac{1}{\sqrt{5}}$=$\frac{\sqrt{5}}{5}$，∴$\frac{2\sqrt{5}}{5}$≤cosθ＜1．
∴$\frac{3}{5}$≤2cos²θ-1＜1，即$\frac{3}{5}$≤cos2θ＜1．
$\overrightarrow{PA}•\overrightarrow{PB}$=$\frac{1}{ta{n}^{2}θ}$cos2θ=$\frac{1+cos2θ}{1-cos2θ}$•cos2θ，
设t=cos2θ，f（t）=$\frac{1+t}{1-t}•t$，
则f′（t）=$\frac{-{t}^{2}+2t+1}{（1-t）^{2}}$，令f′（t）=0得t=1-$\sqrt{2}$或1+$\sqrt{2}$，
∴当1-$\sqrt{2}$$＜t＜1+\sqrt{2}$时，f′（t）＞0，
∴f（t）在[$\frac{3}{5}$，1）上单调递增，
又f（$\frac{3}{5}$）=$\frac{12}{5}$，当t→1时，f（t）→+∞，
∴f（t）≥$\frac{12}{5}$．
故答案为：[$\frac{12}{5}$，+∞）．

点评 本题考查圆的切线的性质、三角函数的二倍角公式、向量的数量积公式、基本不等式求函数的最值，属于中档题