题目内容
6.给出下列命题:①函数y=sin2x偶函数;
②函数y=sin2x的最小正周期为π;
③函数y=ln(x+1)没有零点;
④函数y=ln(x+1)在区间(-1,0)上是增函数.
其中正确的命题是②④(只填序号)
分析 由正弦函数的奇偶性即可判断则y=sin2x奇函数,故①错误; 由y=sin2x的最小正周期为T=$\frac{2π}{ω}$=π,故②正确;当x=0时,y=ln(x+1)=0,故函数存在零点,故③错误; 函数y=ln(x+1)在区间(-1,+∞)上单调递增,故函数y=ln(x+1)在区间(-1,0)上是增函数,④正确,即可求得答案.
解答 解:由正弦函数的性质可知:f(x)=y=sin2x,则f(-x)=sin(-2x)=-sin2x=-f(x),则y=sin2x奇函数,故①错误;
由y=sin2x的最小正周期为T=$\frac{2π}{ω}$=π,故②正确;
令函数y=ln(x+1)=0,即x+1=1,x=0,函数存在零点,故③错误;
由对数函数的单调性可知:函数y=ln(x+1)在区间(-1,+∞)上单调递增,
故函数y=ln(x+1)在区间(-1,0)上是增函数,④正确.
故答案为:②④
点评 本题考查正弦函数的性质,考查对数函数的单调性即零点存在定义,考查计算能力,属于基础题.

练习册系列答案
相关题目
16.
(1)画出散点图.观察散点图,说明两个变量有怎样的相关性.
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.参考公式:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$
(3)当销售额为4(千万元)时,估计利润额的大小.
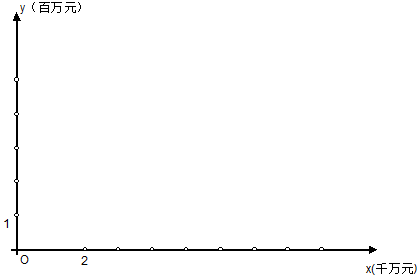
| 商品名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(百万元) | 2 | 3 | 3 | 4 | 5 |
(2)用最小二乘法计算利润额y对销售额x的回归直线方程.参考公式:
$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$
(3)当销售额为4(千万元)时,估计利润额的大小.

11.在△ABC 中,A=30°,a=3,b=4,那么满足条件的△ABC 个数有( )
| A. | 不存在 | B. | 不能确定 | C. | 一个 | D. | 两个 |
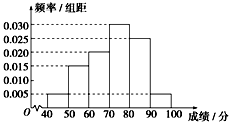 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩 (均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72,众数为75.
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩 (均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72,众数为75.