题目内容
判断函数增减性：f（x）=3x-
．
| 6 |
| x |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：首先，确定函数的定义域，然后，利用单调性的定义，进行逐个区间判断即可．
解答：
解：因为函数：f（x）=3x-
，
∴x≠0，
∴函数的定义域为（-∞，0）∪（0，+∞），
函数在（-∞，0）和（0，+∞）上为增函数，
证明如下：
先证明函数在（-∞，0）上为增函数，
任由设x1，x2∈（-∞，0），x1＜x2，
∴f(x1)-f(x2)=3x1-
-3x2+
，
=3(x1-x2)+
，
=(x1-x2)(3+
)，
∵x1＜x2，
∴x1-x2＜0，
∵x1＜0，x2＜0，
∴3+
＞0，
∴f（x1）＜f（x2），
∴函数在（-∞，0）上为增函数，
同理可以证明 函数在（0，+∞）上为增函数，
| 6 |
| x |
∴x≠0，
∴函数的定义域为（-∞，0）∪（0，+∞），
函数在（-∞，0）和（0，+∞）上为增函数，
证明如下：
先证明函数在（-∞，0）上为增函数，
任由设x1，x2∈（-∞，0），x1＜x2，
∴f(x1)-f(x2)=3x1-
| 6 |
| x1 |
| 6 |
| x2 |
=3(x1-x2)+
| 6(x1-x2) |
| x1x2 |
=(x1-x2)(3+
| 6 |
| x1 x2 |
∵x1＜x2，
∴x1-x2＜0，
∵x1＜0，x2＜0，
∴3+
| 6 |
| x1 x2 |
∴f（x1）＜f（x2），
∴函数在（-∞，0）上为增函数，
同理可以证明 函数在（0，+∞）上为增函数，
点评：本题主要考查函数单调性定义，注意函数的定义域求解方法．
练习册系列答案
相关题目
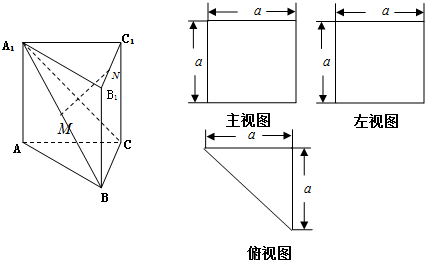一个多面体的直观图、主视图、左视图、俯视图如图，M、N分别为A1B、B1C1的中点．下列结论中正确的个数有（ ）