题目内容
已知数列{an}的前n项和为Sn,且a1+2a2+3a3+…+nan=(n-1)Sn+2n(n∈N*),求数列{an}通项公式.
考点:数列递推式,等比关系的确定
专题:综合题,等差数列与等比数列
分析:根据a1+2a2+3a3+…+nan=(n-1)Sn+2n(n∈N*),再写一式,两式相减,化简可得{Sn+2}是以4为首项,2为公比的等比数列,求出Sn=2n+1-2,即可得到结论.
解答:
解:∵a1+2a2+3a3+…+nan=(n-1)Sn+2n(n∈N*),①
∴当n≥2时,a1+2a2+3a3+…+(n-1)an-1=(n-2)Sn-1+2(n-1).②
①-②得nan=(n-1)Sn-(n-2)Sn-1+2
∴nan=n(Sn-Sn-1)-Sn+2Sn-1+2
∴nan=nan-Sn+2Sn-1+2.
∴-Sn+2Sn-1+2=0,即Sn=2Sn-1+2,
∴Sn+2=2(Sn-1+2).
∵S1+2=4≠0,∴Sn-1+2≠0,
∴{Sn+2}是以4为首项,2为公比的等比数列.
∴Sn+2=2n+1,
∴Sn=2n+1-2,
∴n≥2时,an=Sn-Sn-1=2n,
n=1时,a1=S1=2,也满足上式,
∴an=2n.
∴当n≥2时,a1+2a2+3a3+…+(n-1)an-1=(n-2)Sn-1+2(n-1).②
①-②得nan=(n-1)Sn-(n-2)Sn-1+2
∴nan=n(Sn-Sn-1)-Sn+2Sn-1+2
∴nan=nan-Sn+2Sn-1+2.
∴-Sn+2Sn-1+2=0,即Sn=2Sn-1+2,
∴Sn+2=2(Sn-1+2).
∵S1+2=4≠0,∴Sn-1+2≠0,
∴{Sn+2}是以4为首项,2为公比的等比数列.
∴Sn+2=2n+1,
∴Sn=2n+1-2,
∴n≥2时,an=Sn-Sn-1=2n,
n=1时,a1=S1=2,也满足上式,
∴an=2n.
点评:本题考查数列递推式,考查等比数列的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
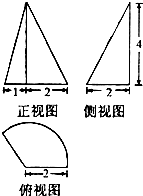
某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
复数(
+
i)2的共轭复数是( )
| 1 |
| 2 |
| ||
| 2 |
A、-
| ||||||
B、
| ||||||
C、
| ||||||
D、-
|
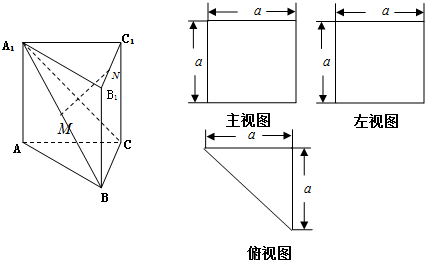 一个多面体的直观图、主视图、左视图、俯视图如图,M、N分别为A1B、B1C1的中点.下列结论中正确的个数有( )
一个多面体的直观图、主视图、左视图、俯视图如图,M、N分别为A1B、B1C1的中点.下列结论中正确的个数有( )