题目内容
过点A（4，1）且与圆（x-1）2+y2=1相切的直线方程是 ．
考点：圆的切线方程
专题：直线与圆
分析：设出圆的切线方程，由圆心到切线的距离等于圆的半径列式求斜率，则切线方程可求．
解答：
解：设过点A（4，1）的圆的切线方程为y-1=k（x-4），即kx-y-4k+1=0，
圆（x-1）2+y2=1的圆心为（1，0），半径为1，
由圆心到切线的距离等于半径得
=1，解得：k=0或k=
．
当k=0时，切线方程为：y=1；
当k=
时，切线方程为：3x-4y-8=0．
故答案为：y=1或3x-4y-8=0．
圆（x-1）2+y2=1的圆心为（1，0），半径为1，
由圆心到切线的距离等于半径得
| |k-4k+1| | ||
|
| 3 |
| 4 |
当k=0时，切线方程为：y=1；
当k=
| 3 |
| 4 |
故答案为：y=1或3x-4y-8=0．
点评：本题考查了圆的切线方程，训练了点到直线的距离公式，是中档题．
练习册系列答案
相关题目
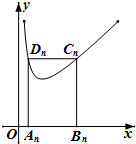如图，矩形AnBnCnDn的一边AnBn在x轴上，另外两个顶点CnDn在函数f（x）=x+
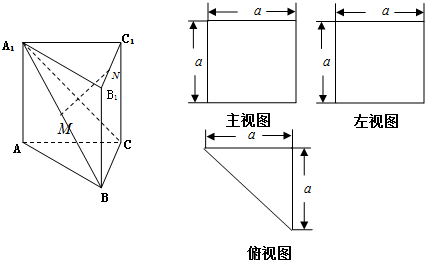一个多面体的直观图、主视图、左视图、俯视图如图，M、N分别为A1B、B1C1的中点．下列结论中正确的个数有（ ）