题目内容
若向量 =(1,0),向量
=(1,0),向量 =(1,1),则
=(1,1),则 -
- =________,
=________, -
- 与
与 的夹角为________.
的夹角为________.
(0,-1) 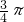
分析:由条件求得 -
- 的坐标,设
的坐标,设  -
- 与
与 的夹角为θ,0≤θ≤π,利用两个向量的夹角公式求得cosθ=
的夹角为θ,0≤θ≤π,利用两个向量的夹角公式求得cosθ= 的值,即可求得
的值,即可求得 -
- 与
与 的夹角.
的夹角.
解答:∵向量 =(1,0),向量
=(1,0),向量 =(1,1),∴
=(1,1),∴ -
- =(1,0)-(1,1)=(0,-1).
=(1,0)-(1,1)=(0,-1).
设 -
- 与
与 的夹角为θ,0≤θ≤π,由于|
的夹角为θ,0≤θ≤π,由于| |=1,|
|=1,| |=
|= ,(
,( )•
)• =(0,-1)•(1,1)=-1,
=(0,-1)•(1,1)=-1,
故有cosθ= =
= =-
=- ,∴θ=
,∴θ= ,
,
故答案为 (0,-1), .
.
点评:本题主要考查两个向量的夹角公式,两个向量坐标形式的运算,根据三角函数的值求角,属于中档题.
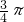
分析:由条件求得
 -
- 的坐标,设
的坐标,设  -
- 与
与 的夹角为θ,0≤θ≤π,利用两个向量的夹角公式求得cosθ=
的夹角为θ,0≤θ≤π,利用两个向量的夹角公式求得cosθ= 的值,即可求得
的值,即可求得 -
- 与
与 的夹角.
的夹角.解答:∵向量
 =(1,0),向量
=(1,0),向量 =(1,1),∴
=(1,1),∴ -
- =(1,0)-(1,1)=(0,-1).
=(1,0)-(1,1)=(0,-1).设
 -
- 与
与 的夹角为θ,0≤θ≤π,由于|
的夹角为θ,0≤θ≤π,由于| |=1,|
|=1,| |=
|= ,(
,( )•
)• =(0,-1)•(1,1)=-1,
=(0,-1)•(1,1)=-1,故有cosθ=
 =
= =-
=- ,∴θ=
,∴θ= ,
,故答案为 (0,-1),
 .
.点评:本题主要考查两个向量的夹角公式,两个向量坐标形式的运算,根据三角函数的值求角,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 =(1,1),向量
=(1,1),向量 与向量
与向量 的夹角为
的夹角为 ,且
,且 =-1.
=-1. ;
;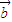 与
与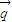 =(1,0)的夹角为
=(1,0)的夹角为 ,向量
,向量 =(cosA,2cos2
=(cosA,2cos2 ),其中A,C为△ABC的内角,且A+C=
),其中A,C为△ABC的内角,且A+C= ,求|
,求| |的最小值.
|的最小值. =(1,1),向量
=(1,1),向量 与向量
与向量 的夹角为
的夹角为 ,且
,且 =-1.
=-1. ;
; 与
与 =(1,0)的夹角为
=(1,0)的夹角为 ,向量
,向量 =(cosA,2cos2
=(cosA,2cos2 ),其中A,C为△ABC的内角,且A+C=
),其中A,C为△ABC的内角,且A+C= ,求|
,求| |的最小值.
|的最小值.