题目内容
已知向量 =(1,1),向量
=(1,1),向量 与向量
与向量 的夹角为
的夹角为 ,且
,且 =-1.
=-1.(1)求向量
 ;
;(2)若向量
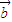 与
与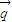 =(1,0)的夹角为
=(1,0)的夹角为 ,向量
,向量 =(cosA,2cos2
=(cosA,2cos2 ),其中A,C为△ABC的内角,且A+C=
),其中A,C为△ABC的内角,且A+C= ,求|
,求| |的最小值.
|的最小值.
【答案】分析:(1)设 =(x,y),由
=(x,y),由 =-1,可得x+y=-1.再由
=-1,可得x+y=-1.再由  =|
=| ||
|| |cos
|cos ,化简可得 x2+y2=1,求得x、y的值,可得
,化简可得 x2+y2=1,求得x、y的值,可得 的值.
的值.
(2)由条件可得 =(0,-1),又因为
=(0,-1),又因为  =(cosA,cosC),求得|
=(cosA,cosC),求得| +
+ |2=1+
|2=1+ cos(2A+
cos(2A+ ).结合A的范围,可得|
).结合A的范围,可得| |取得最小值.
|取得最小值.
解答:解:(1)设 =(x,y),
=(x,y), =-1,可得x+y=-1. ①…(2分)
=-1,可得x+y=-1. ①…(2分)
又 与
与 的夹角为
的夹角为 ,所以
,所以  =|
=| ||
|| |cos
|cos ,化简可得 x2+y2=1. ②
,化简可得 x2+y2=1. ②
由①②解得 ,或
,或 ,
,
故 =(-1,0),或
=(-1,0),或 =(-1,0).…(6分)
=(-1,0).…(6分)
(2)由向量 与
与 垂直知
垂直知 =(0,-1),由 A+C=
=(0,-1),由 A+C= 可得 0<A<
可得 0<A< .…(8分)
.…(8分)
又因为 =(cosA,2
=(cosA,2 -1)=(cosA,cosC),
-1)=(cosA,cosC),
所以| +
+ |2=cos2A+cos2C=
|2=cos2A+cos2C= +
+ =1+
=1+ [cos2A+cos(
[cos2A+cos( -2A)]
-2A)]
=1+ cos2A-
cos2A- sin2A=1+
sin2A=1+ cos(2A+
cos(2A+ ).
).
再由 <A+
<A+ <
< ,可得当A+
,可得当A+ =π时,|
=π时,| |取得最小值为
|取得最小值为  =
= .
.
点评:本题主要考查两个向量的数量积公式,三角函数的恒等变换及化简求值,属于中档题.
 =(x,y),由
=(x,y),由 =-1,可得x+y=-1.再由
=-1,可得x+y=-1.再由  =|
=| ||
|| |cos
|cos ,化简可得 x2+y2=1,求得x、y的值,可得
,化简可得 x2+y2=1,求得x、y的值,可得 的值.
的值.(2)由条件可得
 =(0,-1),又因为
=(0,-1),又因为  =(cosA,cosC),求得|
=(cosA,cosC),求得| +
+ |2=1+
|2=1+ cos(2A+
cos(2A+ ).结合A的范围,可得|
).结合A的范围,可得| |取得最小值.
|取得最小值.解答:解:(1)设
 =(x,y),
=(x,y), =-1,可得x+y=-1. ①…(2分)
=-1,可得x+y=-1. ①…(2分)又
 与
与 的夹角为
的夹角为 ,所以
,所以  =|
=| ||
|| |cos
|cos ,化简可得 x2+y2=1. ②
,化简可得 x2+y2=1. ②由①②解得
 ,或
,或 ,
,故
 =(-1,0),或
=(-1,0),或 =(-1,0).…(6分)
=(-1,0).…(6分)(2)由向量
 与
与 垂直知
垂直知 =(0,-1),由 A+C=
=(0,-1),由 A+C= 可得 0<A<
可得 0<A< .…(8分)
.…(8分)又因为
 =(cosA,2
=(cosA,2 -1)=(cosA,cosC),
-1)=(cosA,cosC),所以|
 +
+ |2=cos2A+cos2C=
|2=cos2A+cos2C= +
+ =1+
=1+ [cos2A+cos(
[cos2A+cos( -2A)]
-2A)]=1+
 cos2A-
cos2A- sin2A=1+
sin2A=1+ cos(2A+
cos(2A+ ).
).再由
 <A+
<A+ <
< ,可得当A+
,可得当A+ =π时,|
=π时,| |取得最小值为
|取得最小值为  =
= .
.点评:本题主要考查两个向量的数量积公式,三角函数的恒等变换及化简求值,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目