题目内容
若不全为0的实数k1,k2…kn满足k1
1+k2
2+…+kn
n=0,则称向量
1,
2,…
n为”线性相关”.依据此规定,若向量
1=(1,0),
2=(1,1),
3=(2,2)线性相关,则k1,k2,k3的取值依次可以为
| a |
| a |
| a |
| a |
| a |
| a |
| a |
| a |
| a |
0,-2,1
0,-2,1
(写一组数即可)分析:先利用题中的定义设出方程,然后根据向量的坐标运算得到方程组,给其中一个未知数赋值求出方程组的一个解即可.
解答:解:根据题意可设k1
+k2
+k3
=
,
则
化简得
当k3=1时,k1=0,k2=-2
故答案为:0,-2,1
| a1 |
| a2 |
| a3 |
| 0 |
则
|
化简得
|
当k3=1时,k1=0,k2=-2
故答案为:0,-2,1
点评:本题主要考查了新定义,以及向量的坐标运算和平面向量的基本定理,同时考查了赋值法解不定方程,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
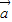 1+k2
1+k2 2+…+kn
2+…+kn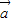 n=0,则称向量
n=0,则称向量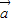 1,
1,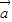 2,…
2,… n为”线性相关”.依据此规定,若向量
n为”线性相关”.依据此规定,若向量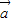 1=(1,0),
1=(1,0),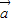 2=(1,1),
2=(1,1), 3=(2,2)线性相关,则k1,k2,k3的取值依次可以为 (写一组数即可)
3=(2,2)线性相关,则k1,k2,k3的取值依次可以为 (写一组数即可)