题目内容
若不全为0的实数k1,k2…kn满足k1
1+k2
2+…+kn
n=0,则称向量
1,
2,…
n为”线性相关”.依据此规定,若向量
1=(1,0),
2=(1,1),
3=(2,2)线性相关,则k1,k2,k3的取值依次可以为______ (写一组数即可)
| a |
| a |
| a |
| a |
| a |
| a |
| a |
| a |
| a |
根据题意可设k1
+k2
+k3
=
,
则
化简得
当k3=1时,k1=0,k2=-2
故答案为:0,-2,1
| a1 |
| a2 |
| a3 |
| 0 |
则
|
化简得
|
当k3=1时,k1=0,k2=-2
故答案为:0,-2,1

练习册系列答案
相关题目
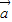 1+k2
1+k2 2+…+kn
2+…+kn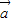 n=0,则称向量
n=0,则称向量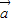 1,
1,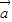 2,…
2,… n为”线性相关”.依据此规定,若向量
n为”线性相关”.依据此规定,若向量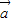 1=(1,0),
1=(1,0),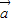 2=(1,1),
2=(1,1), 3=(2,2)线性相关,则k1,k2,k3的取值依次可以为 (写一组数即可)
3=(2,2)线性相关,则k1,k2,k3的取值依次可以为 (写一组数即可)