题目内容
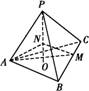
如图,三棱锥P
ABC的高PO=8,AC=BC=3,
∠ACB=30°,M,N分别在BC和PO上,且CM=x,PN=2CM,则三棱锥NAMC的体积V在x∈(0,3]上的最大体积是 .
2解析:
=
S△AMC·NO
=×
AC·CMsin 30°·(PO-PN)
=××3x×(8-2x)
=(4x-x2)
=2-(x-2)2,
因为x∈(0,3],
所以三棱锥NAMC的最大体积是2.
练习册系列答案
相关题目
题目内容
如图,三棱锥PABC的高PO=8,AC=BC=3,
∠ACB=30°,M,N分别在BC和PO上,且CM=x,PN=2CM,则三棱锥NAMC的体积V在x∈(0,3]上的最大体积是 .
2解析:=S△AMC·NO
=×AC·CMsin 30°·(PO-PN)
=××3x×(8-2x)
=(4x-x2)
=2-(x-2)2,
因为x∈(0,3],
所以三棱锥NAMC的最大体积是2.
满足
，则
的取值范围是（ ）
+
(B)
+
CDE的体积.
A1B1C1D1中,O是底面正方形ABCD的中心,M是D1D的中点,N是A1B1的中点,则直线NO、AM的位置关系是( )