题目内容
如图,直角梯形ACDE与等腰直角△ABC所在平面互相垂直,F为BC的中点,∠BAC=∠ACD=90°,AE∥CD,DC=AC=2AE=2.
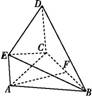
(1)求证:AF∥平面BDE;
(2)求四面体B CDE的体积.
CDE的体积.
1)证明:取BD的中点P,
连接EP、FP,

则PF为中位线,PF
 DC,
DC,
又∵EA
 DC,
DC,
∴EA PF.
PF.
故四边形AFPE是平行四边形,即AF∥EP.
∵EP⊂平面BDE,AF⊄平面BDE,
∴AF∥平面BDE.
(2)解:∵BA⊥AC,平面ABC⊥平面ACDE且交于AC,
∴BA⊥平面ACDE,即BA就是四面体B CDE的高,
CDE的高,
BA=AC=2.
∵DC=AC=2AE=2,AE∥CD,
∴S梯形ACDE= ×(1+2)×2=3,
×(1+2)×2=3,
S△ACE= ×AE×AC=
×AE×AC= ×1×2=1,
×1×2=1,
∴S△CDE=3-1=2,
∴ =
= ·BA·S△CDE
·BA·S△CDE
= ×2×2=
×2×2= .
.

练习册系列答案
相关题目
 ,求函数
,求函数 的最小值。
的最小值。 ABC的高PO=8,AC=BC=3,
ABC的高PO=8,AC=BC=3,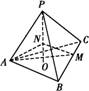
 A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是 (写出所有正确命题的编号).
A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是 (写出所有正确命题的编号). 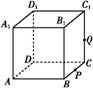
 时,S为四边形;
时,S为四边形; 时,S与C1D1的交点R满足C1R=
时,S与C1D1的交点R满足C1R= ;
;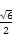 .
.

 A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E.要使AB1⊥平面C1DF,则线段B1F的长为( )
A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E.要使AB1⊥平面C1DF,则线段B1F的长为( )
 (B)1
(B)1 (D)2
(D)2