题目内容
A是△BCD所在平面外的一点,E,F分别是BC,AD的中点.
(1)求证:直线EF与BD是异面直线;
(2)若AC⊥BD,AC=BD,求EF与BD所成的角.
(1)证明:假设EF与BD不是异面直线,则EF与BD共面,从而DF与BE共面,即AD与BC共面,所以A,B,C,D在同一平面内,这与A是△BCD所在平面外的一点相矛盾,故直线EF与BD是异面直线.

(2)解:取CD的中点G,连接EG,FG,则EG∥BD,
所以相交直线EF与EG所成的角,即为异面直线EF与BD所成的角.
在Rt△EGF中,由EG=FG= AC,求得∠FEG=45°,
AC,求得∠FEG=45°,
即异面直线EF与BD所成的角为45°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的最大值为________.
的最大值为________.

 ABC的高PO=8,AC=BC=3,
ABC的高PO=8,AC=BC=3,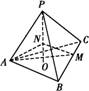
 A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是 (写出所有正确命题的编号).
A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是 (写出所有正确命题的编号). 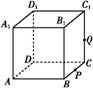
 时,S与C1D1的交点R满足C1R=
时,S与C1D1的交点R满足C1R= ;
;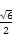 .
.
 A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E.要使AB1⊥平面C1DF,则线段B1F的长为( )
A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E.要使AB1⊥平面C1DF,则线段B1F的长为( )
 (B)1
(B)1 (D)2
(D)2 ,则
,则 ·
· 的值是( )
的值是( ) B.
B. D.0
D.0