题目内容
16.在$△ABC中,∠A=\frac{π}{3},且({\overrightarrow{AB}+\overrightarrow{AC}})•\overrightarrow{BC}=0$,点M是△ABC外一点,BM=2CM=2,则AM的最大值与最小值的差为2.分析 取边BC的中点为O,把($\overrightarrow{AB}$+$\overrightarrow{AC}$)•$\overrightarrow{BC}$=0转化为$\overrightarrow{AO}$•$\overrightarrow{BC}$=0,得出$\overrightarrow{AO}$⊥$\overrightarrow{BC}$,△ABC为等边三角形,以O为坐标原点,以BC边所在的直线为x轴,建立平面直角坐标系,利用坐标表示得出AM的解析式,求出它的最大值与最小值即可.
解答 解:取边BC的中点为O,则$\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AC}$),
又($\overrightarrow{AB}$+$\overrightarrow{AC}$)•$\overrightarrow{BC}$=0,∴$\overrightarrow{AO}$•$\overrightarrow{BC}$=0,
∴$\overrightarrow{AO}$⊥$\overrightarrow{BC}$,∴△ABC为等腰三角形,
又∠A=$\frac{π}{3}$,∴△ABC为等边三角形,
以O为坐标原点,以BC边所在的直线为x轴,
建立平面直角坐标系如图所示;
并设BC=2a($\frac{1}{2}$<a<$\frac{3}{2}$),点M(x,y);
则A(0,$\sqrt{3}$a),B(-a,0),C(a,0),
又BM=2CM=2,
所以(x+a)2+y2=4
(x-a)2+y2=1,
所以解方程组$\left\{\begin{array}{l}{{(x+a)}^{2}{+y}^{2}=4}\\{{(x-a)}^{2}{+y}^{2}=1}\end{array}\right.$得:$\left\{\begin{array}{l}{x=\frac{3}{4a}}\\{y=\sqrt{1{-(\frac{3}{4a}-a)}^{2}}}\end{array}\right.$ 或$\left\{\begin{array}{l}{x=\frac{3}{4a}}\\{y=-\sqrt{1{-(\frac{3}{4a}-a)}^{2}}}\end{array}\right.$,
所以当$\left\{\begin{array}{l}{x=\frac{3}{4a}}\\{y=\sqrt{1{-(\frac{3}{4a}-a)}^{2}}}\end{array}\right.$时$AM=\sqrt{{{(\frac{3}{4a})}^2}+{{[\sqrt{3}a-\sqrt{1-{{(\frac{3}{4a}-a)}^2}}]}^2}}$
=$\sqrt{{(\frac{3}{4a})}^{2}+{3a}^{2}+1{-(\frac{3}{4a}-a)}^{2}-2\sqrt{3}×\sqrt{{a}^{2}{-(\frac{3}{4}{-a}^{2})}^{2}}}$
=$\sqrt{{2a}^{2}+\frac{5}{2}-2\sqrt{3}×\sqrt{{-a}^{4}+{\frac{5}{2}a}^{2}-\frac{9}{16}}}$
=$\sqrt{{2a}^{2}+\frac{5}{2}-2\sqrt{3}×\sqrt{1{-{(a}^{2}-\frac{5}{4})}^{2}}}$,
令a2-$\frac{5}{4}$=cosθ,
则AM=$\sqrt{5+2cosθ-2\sqrt{3}sinθ}$=$\sqrt{5-4sin(θ-\frac{π}{6})}$,
所以当θ=$\frac{2π}{3}$ 时(AM)min=1,
同理当$\left\{\begin{array}{l}{x=\frac{3}{4a}}\\{y=-\sqrt{1{-(\frac{3}{4a}-a)}^{2}}}\end{array}\right.$时,
AM=$\sqrt{{2a}^{2}+\frac{5}{2}+2\sqrt{3}×\sqrt{1{-{(a}^{2}-\frac{5}{4})}^{2}}}$=$\sqrt{5+2cosθ+2\sqrt{3}sinθ}$=$\sqrt{5+4sin(θ+\frac{π}{6})}$,
所以当θ=$\frac{π}{3}$时(AM)max=3;
综上可知:AM的取值范围是[1,3],
AM的最大值与最小值的差是2.
故答案为:2.
点评 本题考查了平面向量的数量积与应用问题,也考查了数形结合与逻辑推理以及计算能力的应用问题,是难题.

| A. | -i | B. | $\frac{4}{5}-\frac{3}{5}$i | C. | i | D. | $\frac{4}{3}$-i |
| A. | f1(x)与f3(x) | B. | f2(x)与f4(x) | C. | f1(x)与f2(x) | D. | f3(x)与f4(x) |
| A. | -14 | B. | -7 | C. | 14 | D. | 7 |
| A. | {1,2} | B. | {1,2,3} | C. | {4,5} | D. | {3,4,5} |
| A. | (-∞,$\frac{1}{e}$) | B. | (-∞,$\frac{1}{\sqrt{e}}$) | C. | (-∞,$\sqrt{e}$) | D. | (-∞,e) |
| A. | $\frac{e}{2}$ | B. | e | C. | e-1 | D. | $\frac{e}{2}$-1 |
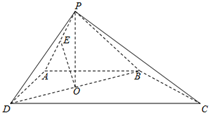 如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的一动点.
如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的一动点.