题目内容
5.在研究函数 f ( x )=$\sqrt{{x^2}+4}$-$\sqrt{{x^2}-12x+40}$的性质时,某同学受两点间距离公式启发,将f(x)变形为f(x)=$\sqrt{(x-0{)^2}+(0-2{)^2}}$-$\sqrt{(x-6{)^2}+(0-2{)^2}}$,并给出关于函数f(x)以下五个描述:①函数 f(x)的图象是中心对称图形;
②函数 f(x)的图象是轴对称图形;
③函数 f(x)在[0,6]上是增函数;
④函数 f(x)没有最大值也没有最小值;
⑤无论m为何实数,关于x的方程 f(x)-m=0都有实数根.
其中描述正确的是①③④.
分析 函数 f ( x )=$\sqrt{{x^2}+4}$-$\sqrt{{x^2}-12x+40}$=$\sqrt{(x-0{)^2}+(0-2{)^2}}$-$\sqrt{(x-6{)^2}+(0-2{)^2}}$,如图表示点P(x,0)到点A(0,2)的距离|PA|与到点B(6,2)的距离|PB|之差;结合图形可知,在x=3处,f(x)=0,-6<PA-PB<6
∴函数 f(x)的图象是中心对称图形,对称中心为(3,0),即可判断.
解答 解:函数 f ( x )=$\sqrt{{x^2}+4}$-$\sqrt{{x^2}-12x+40}$=$\sqrt{(x-0{)^2}+(0-2{)^2}}$-$\sqrt{(x-6{)^2}+(0-2{)^2}}$,如图表示点P(x,0)到点A(0,2)的距离|PA|与到点B(6,2)的距离|PB|之差;结合图形可知,在x=3处,f(x)=0,-6<PA-PB<6
∴函数 f(x)的图象是中心对称图形,对称中心为(3,0),故①正确,②错;
在(-∞,+∞)递增,值域为(-6,6)
故③,函数 f(x)在[0,6]上是增函数,正确;
故④函数 f(x)没有最大值也没有最小值,正确;
故⑤无论m为何实数,关于x的方程 f(x)-m=0都有有实数根,错.
故答案为:①③④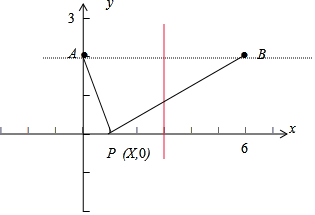
点评 本题考查了函数表达式的几何意义,属于中档题.

练习册系列答案
相关题目
16.已知全集U=R,集合A={x|y=lgx},集合B=$\left\{{y|y=\sqrt{x}+1}\right\}$,那么A∩(∁UB)=( )
| A. | ∅ | B. | (0,1] | C. | (0,1) | D. | (1,+∞) |
20.已知 x,y 满足不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ x+y≤m\\ y+2x≤4\end{array}\right.$,当 3≤m≤5 时,目标函数 z=3x+2y的最大值的变化范围是( )
| A. | [7,8] | B. | [7,15] | C. | [6,8] | D. | [6,15] |
10.下列结论中错误的是( )
| A. | 若0<α<$\frac{π}{2}$,则sinα<tanα | |
| B. | 若α是第二象限角,则$\frac{α}{2}$为第一象限或第三象限角 | |
| C. | 若角α的终边过点P(3k,4k)(k≠0),则sinα=$\frac{4}{5}$ | |
| D. | 若扇形的周长为6,半径为2,则其中心角的大小为1弧度 |
13.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足:|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=4,<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$,则|3$\overrightarrow{a}$-2$\overrightarrow{b}$|=( )
| A. | 52 | B. | $2\sqrt{13}$ | C. | 100-48$\sqrt{3}$ | D. | $\sqrt{100-48\sqrt{3}}$ |
 ,
, ,
, ,
, ,
, ,若
,若 ,则
,则 的最小值是( )
的最小值是( ) B.
B. C.
C. D.
D.