题目内容
18. 如图,多面体SABCD中面ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,SD=$\sqrt{3}$AD.
如图,多面体SABCD中面ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,SD=$\sqrt{3}$AD.(I)求证:面SDB⊥面ABCD.
(Ⅱ)求面SBD与面SAB所成的二面角的正弦值.
分析 (I)直接根据条件得到SD⊥平面ABCD,然后根据面面垂直的判定定理即可证明结论;
(II)先建立空间直角坐标系,求出各点的坐标,进而求出两个半平面的法向量,再代入向量的夹角计算公式即可.
解答 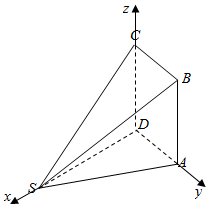 解:(I)∵SD⊥AD,SD⊥AB,AB∩AB=A,
解:(I)∵SD⊥AD,SD⊥AB,AB∩AB=A,
∴SD⊥平面ABCD …(2分)
∵SD?面SDB,
∴面SDB⊥面ABCD …(5分)
(II)如图建立空间直角坐标系,
∵AD=a(a>0),AB=2AD,SD=$\sqrt{3}$AD,
∴S($\sqrt{3}$a,0,0),A(0,a,0),B(0,a,2a),C(0,0,2a),D(0,0,0).
∴$\overrightarrow{DS}$=($\sqrt{3}$a,0,0),$\overrightarrow{DB}$=(0,a,2a)
设面SBD的一个法向量为$\overrightarrow{n}$=(x,y,z)
∴$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DS}=0}\\{\overrightarrow{n}•\overrightarrow{DB}=0}\end{array}\right.$?$\left\{\begin{array}{l}{\sqrt{3}ax=0}\\{ay+2az=0}\end{array}\right.$⇒$\overrightarrow{n}$=(0,2,-1)…(9分)
又∵$\overrightarrow{AB}$=(0,0,2a),$\overrightarrow{SA}$=(-$\sqrt{3}$a,a,0)
设面SAB的一个法向量为$\overrightarrow{m}$=(x,y,z).
∴$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AB}=0}\\{\overrightarrow{m}•\overrightarrow{SA}=0}\end{array}\right.$?$\left\{\begin{array}{l}{2az=0}\\{-\sqrt{3}ax+ay=0}\end{array}\right.$⇒$\overrightarrow{m}$=(1,$\sqrt{3}$,0).
∴cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{0×1+(-2)×\sqrt{3}+1×0}{\sqrt{5}×\;2}$=$\frac{0×1+2×\sqrt{3}+(-1)×0}{\sqrt{5}×\;2}$=$\frac{\sqrt{15}}{5}$,
∴所以所求的二面角的正弦值为$\sqrt{1-(\frac{\sqrt{15}}{5})^{2}}$=$\frac{\sqrt{10}}{5}$…(14分)
点评 本题主要考查面面垂直的判断以及利用空间向量求平面间的夹角.解决问题的关键在于先建立空间直角坐标系,求出各点的坐标,进而求出两个半平面的法向量.

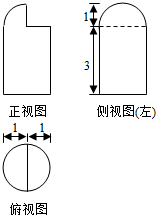
| A. | $\frac{17π}{2}$ | B. | 9π | C. | $\frac{19π}{2}$ | D. | 10π |
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | c<b<a |
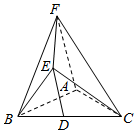 在如图所示的几何体EFABC中,已知△ABC是等腰三角形,AB=AC,AF⊥平面ABC,D为BC的中点,DE∥AF且BC=AF=2DE=2.
在如图所示的几何体EFABC中,已知△ABC是等腰三角形,AB=AC,AF⊥平面ABC,D为BC的中点,DE∥AF且BC=AF=2DE=2.