题目内容
已知函数f(x)=2x-
(1)判断函数的奇偶性、增减性并证明.
(2)若f(x)中,x=sinα+cosα,α∈(-
,0),且f(1-m)+f(1-m2)<0,求实数m的取值范围.
| 1 |
| 2x |
(1)判断函数的奇偶性、增减性并证明.
(2)若f(x)中,x=sinα+cosα,α∈(-
| π |
| 2 |
考点:奇偶性与单调性的综合,函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用,导数的综合应用,三角函数的求值
分析:根据奇偶性的定义不难判断原函数的奇偶性,增减性的判断通过求函数导数,再判断导函数的符号,即可判断函数f(x)的增减性.
第二问中,先根据a的范围来确定x的范围,这要用到两角和的正弦公式.求出x范围之后,对于1-m,1-m2都要在这个范围中.再根据函数f(x)的奇偶性和单调性,把条件f(1-m)+f(1-m2)<0变成f(1-m)<f(m2-1),并得到1-m<m2-1,结合前面求的关于m的不等式,便可求出m的取值范围.
第二问中,先根据a的范围来确定x的范围,这要用到两角和的正弦公式.求出x范围之后,对于1-m,1-m2都要在这个范围中.再根据函数f(x)的奇偶性和单调性,把条件f(1-m)+f(1-m2)<0变成f(1-m)<f(m2-1),并得到1-m<m2-1,结合前面求的关于m的不等式,便可求出m的取值范围.
解答:
解:原函数的定义域是R.
(1)f(-x)=2-x-
=-(2x-
)=-f(x),
∴函数f(x)是奇函数.
∵f(x)=2x-
=(2x)+(-
),
∴函数f(x)在R上是增函数.
(2)∵x=sina+cosa=
sin(a+
),a∈(-
,0)
∴x∈(-1,1)
又f(1-m)+f(1-m2)<0
∴根据(1)的结论f(x)在R上是奇函数,是增函数;
∴f(1-m)<f(m2-1)
m应该满足:
,解得:1<m<
.
∴m的取值范围是(1,
).
(1)f(-x)=2-x-
| 1 |
| 2-x |
| 1 |
| 2x |
∴函数f(x)是奇函数.
∵f(x)=2x-
| 1 |
| 2x |
| 1 |
| 2x |
∴函数f(x)在R上是增函数.
(2)∵x=sina+cosa=
| 2 |
| π |
| 4 |
| π |
| 2 |
∴x∈(-1,1)
又f(1-m)+f(1-m2)<0
∴根据(1)的结论f(x)在R上是奇函数,是增函数;
∴f(1-m)<f(m2-1)
m应该满足:
|
| 2 |
∴m的取值范围是(1,
| 2 |
点评:本题考查的知识点为函数奇偶性的定义,对于第二问,需要先根据a的范围求出x的范围,从而限制1-m,1-m2的取值在这个范围内.还要注意的是对f(1-m)+f(1-m2)<0的变形处理.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
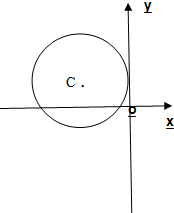 如图,已知位于y轴左侧的圆C与y轴相切于点(0,1),且被x轴分成的两段弧长之比为2:1,过点H(0,t)的直线l与圆C相交于M,N两点,且以MN为直径的圆恰好经过坐标原点O.
如图,已知位于y轴左侧的圆C与y轴相切于点(0,1),且被x轴分成的两段弧长之比为2:1,过点H(0,t)的直线l与圆C相交于M,N两点,且以MN为直径的圆恰好经过坐标原点O. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是平行四边形,∠BAD=60°,AD=2,AC=2
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是平行四边形,∠BAD=60°,AD=2,AC=2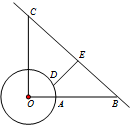 为了适应市场需要,某地准备建一个圆形生猪储备基地(如图),它的附近有一条公路,从基地中心O处向东走1km是储备基地的边界上的点A,接着向东再走7km到达公路上的点B;从基地中心O向正北走8km到达公路的另一点C.现准备在储备基地的边界上选一点D,修建一条由D通往公路BC的专用线DE,则DE的最短距离为
为了适应市场需要,某地准备建一个圆形生猪储备基地(如图),它的附近有一条公路,从基地中心O处向东走1km是储备基地的边界上的点A,接着向东再走7km到达公路上的点B;从基地中心O向正北走8km到达公路的另一点C.现准备在储备基地的边界上选一点D,修建一条由D通往公路BC的专用线DE,则DE的最短距离为