题目内容
已知{an}为等差数列,且a1+a3=8,a2+a4=12.数列{bn}的前n项和为Sn,且3Sn=bn+2,n∈N*,
(1)求数列{an},{bn}的通项公式;
(2)设cn=
,求数列{cn}的前2n+1项的和T2n+1.
(1)求数列{an},{bn}的通项公式;
(2)设cn=
|
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列,点列、递归数列与数学归纳法
分析:(1)根据等差数列的定义建立方程组求出首项和公差即可得到结论.
(2)求出数列{cn}的通项公式,利用分组求和法即可得到结论.
(2)求出数列{cn}的通项公式,利用分组求和法即可得到结论.
解答:
解:(1)∵{an}为等差数列,且a1+a3=8,a2+a4=12.
∴
,解得a1=2,d=2,即an=2+2(n-1)=2n,
∵数列{bn}的前n项和为Sn,且3Sn=bn+2,①
∴当n=1时,3S1=b1+2,解得b1=1,
当n≥2时,3Sn-1=bn-1+2,②
①-②得,bn=-
bn-1,
则数列{bn}是等比数列,公比q=-
,
则bn=(-
)n-1.
(2)cn=
=
,
∴数列{cn}的前2n+1项的和T2n+1=(a1+a3+…+a2n+1)+(b2+b4+…+b2n)
=
•(n+1)+
=2n2+4n+
+
×(
)n.
∴
|
∵数列{bn}的前n项和为Sn,且3Sn=bn+2,①
∴当n=1时,3S1=b1+2,解得b1=1,
当n≥2时,3Sn-1=bn-1+2,②
①-②得,bn=-
| 1 |
| 2 |
则数列{bn}是等比数列,公比q=-
| 1 |
| 2 |
则bn=(-
| 1 |
| 2 |
(2)cn=
|
|
∴数列{cn}的前2n+1项的和T2n+1=(a1+a3+…+a2n+1)+(b2+b4+…+b2n)
=
| 2+2(2n+1) |
| 2 |
(-
| ||||
1-
|
| 4 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
点评:本题主要考查等差数列和等比数列的判断和通项公式的计算,以及数列求和,利用分组求和是解决本题的关键.

练习册系列答案
相关题目
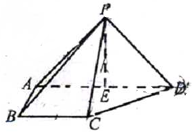 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=