题目内容
12.设复数z的共轭复数为$\overline z$,i为虚数单位,已知(3-4i)$\overline z$=1+2i,则z=$-\frac{1}{5}-\frac{2}{5}i$.分析 把已知等式变形,然后利用复数代数形式的乘除运算化简求得$\overline{z}$,再由共轭复数的概念求得z.
解答 解:由(3-4i)$\overline z$=1+2i,得$\overline{z}=\frac{1+2i}{3-4i}=\frac{(1+2i)(3+4i)}{(3-4i)(3+4i)}=\frac{-5+10i}{25}=-\frac{1}{5}+\frac{2}{5}i$,
∴$z=-\frac{1}{5}-\frac{2}{5}i$.
故答案为:$-\frac{1}{5}-\frac{2}{5}i$.
点评 本题考查复数代数形式的乘除运算,是基础的计算题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
7.已知函数y=f(log2x)的定义域为[1,2],那么函数y=f(x)的定义域为( )
| A. | [2,4] | B. | [1,2] | C. | [0,1] | D. | (0,1] |
4.复数$\frac{2-i}{1-i}$=( )
| A. | $\frac{3}{2}-\frac{i}{2}$ | B. | $\frac{3}{2}+\frac{i}{2}$ | C. | $-\frac{3}{2}+\frac{i}{2}$ | D. | $-\frac{3}{2}-\frac{i}{2}$ |
1.已知集合A={x|y=$\sqrt{x-3}$},B=(0,+∞),则A∩B=( )
| A. | (0,+∞) | B. | (3,+∞) | C. | [0,+∞) | D. | [3,+∞) |
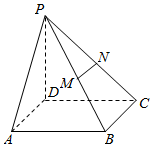 如图,已知四棱锥P-ABCD,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.
如图,已知四棱锥P-ABCD,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.