题目内容
11.在△ABC中,角A,B,C的对边分别为a,b,c,若b=1,$\frac{1}{2}$sinB=cos(B+C)sinC,则当B取得最大值时,△ABC的周长为2+$\sqrt{3}$.分析 由$\frac{1}{2}$sinB=cos(B+C)sinC,利用正弦定理可得:cosA=-$\frac{1}{2c}$<0,A为钝角.因此cosAcosC≠0,由sin(A+C)=sinAcosC+cosAsinC=-2cosAsinC,可得tanA=-3tanC,tanC>0,tanB=-$\frac{tanA+tanC}{1-tanAtanC}$,代入化简整理利用基本不等式的性质即可得出.
解答 解:在△ABC中,∵$\frac{1}{2}$sinB=cos(B+C)sinC,
∴$\frac{1}{2}×1=-ccosA$,即cosA=-$\frac{1}{2c}$<0,∴A为钝角.
∴cosAcosC≠0,
由sin(A+C)=sinAcosC+cosAsinC=-2cosAsinC,
可得tanA=-3tanC,tanC>0,tanB=-$\frac{tanA+tanC}{1-tanAtanC}$=$\frac{-(-2tanC)}{1+3ta{n}^{2}C}$=$\frac{2}{\frac{1}{tanC}+3tanC}$≤$\frac{2}{2\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,当且仅当tanC=$\frac{\sqrt{3}}{3}$时取等号.
∴B取得最大值arctan$\frac{\sqrt{3}}{3}$时,∴c=b=1,C=B=$\frac{π}{6}$.
A=$\frac{2π}{3}$.
∴a=2×$1×cos\frac{π}{6}$=$\sqrt{3}$.
∴a+b+c=2+$\sqrt{3}$.
故答案为:2+$\sqrt{3}$.
点评 本题考查了正弦定理、和差公式、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

 星级口算天天练系列答案
星级口算天天练系列答案| A. | y=-$\frac{{\sqrt{3}}}{3}$x+1 | B. | y=$\frac{{\sqrt{3}}}{3}({x-1})$ | C. | y=-$\frac{{\sqrt{3}}}{3}$x-1 | D. | y=-$\frac{{\sqrt{3}}}{3}({x-1})$ |
| A. | (0,+∞) | B. | (3,+∞) | C. | [0,+∞) | D. | [3,+∞) |
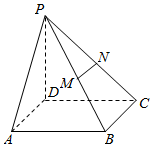 如图,已知四棱锥P-ABCD,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.
如图,已知四棱锥P-ABCD,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.