题目内容
9.下列函数既是奇函数,又在区间(0,+∞)上是增函数的是( )| A. | y=x-1 | B. | y=x2 | C. | y=lgx | D. | y=x3 |
分析 根据函数奇偶性和单调性的性质分别进行判断即可.
解答 解:A.y=x-1为奇函数,在(0,+∞)上是减函数,不满足条件.
B.y=x2是偶函数,当x>0时,函数为增函数,不满足条件.
C.y=lgx定义域为(0,+∞),函数为非奇非偶函数,不满足条件.
D.y=x3是奇函数,在(-∞,+∞)上是增函数,满足条件.
故选:D
点评 本题主要考查函数奇偶性和单调性的判断,要求熟练掌握常见函数奇偶性和单调性的性质.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
19.到两定点(-2,0),(2,0)的距离之差的绝对值为定值3的点的轨迹是( )
| A. | 椭圆 | B. | 线段 | C. | 直线 | D. | 双曲线 |
17.已知点M是椭圆$\frac{x^2}{4}+{y^2}=1$上一点,F1,F2是椭圆的焦点,且满足$\overrightarrow{M{F}_{1}}$•$\overrightarrow{M{F}_{2}}$=0,则△MF1F2的面积为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
4.已知向量$\overrightarrow a=(\;t,\;1)$和$\overrightarrow b=(-2,\;t+2)$,若$\overrightarrow a⊥\overrightarrow b$,则$|\overrightarrow a+\overrightarrow b|$=( )
| A. | 64 | B. | 8 | C. | 5 | D. | $\sqrt{10}$ |
18.若复数z满足$z=\frac{2+i}{i}$(其中i为虚数单位),则$\overline z$=( )
| A. | -1+2i | B. | -1-2i | C. | 1-2i | D. | 1+2i |
5.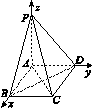 如图,已知四边形ABCD为矩形,PA⊥平面ABCD,连接AC,BD,PB,PC,PD,则下列各组向量中,数量积不一定为零的是( )
如图,已知四边形ABCD为矩形,PA⊥平面ABCD,连接AC,BD,PB,PC,PD,则下列各组向量中,数量积不一定为零的是( )
 如图,已知四边形ABCD为矩形,PA⊥平面ABCD,连接AC,BD,PB,PC,PD,则下列各组向量中,数量积不一定为零的是( )
如图,已知四边形ABCD为矩形,PA⊥平面ABCD,连接AC,BD,PB,PC,PD,则下列各组向量中,数量积不一定为零的是( )| A. | $\overrightarrow{PC}$与$\overrightarrow{BD}$ | B. | $\overrightarrow{DA}$与$\overrightarrow{PB}$ | C. | $\overrightarrow{PD}$与$\overrightarrow{AB}$ | D. | $\overrightarrow{PA}$与$\overrightarrow{CD}$ |
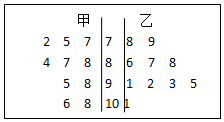 在某次考试中,从甲、乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示.
在某次考试中,从甲、乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示.