题目内容
2.已知函数f(x)满足f(x)=ex-f'(0)x+1,则f(x)=ex-$\frac{1}{2}$x+1.分析 把给出的函数求导,在导函数中取x=0可求出f′(0)=$\frac{1}{2}$,则函数解析式可求.
解答 解:∵f′(x)=ex-f'(0),
∴f′(0)=1-f'(0),
∴f′(0)=$\frac{1}{2}$,
∴f(x)=ex-$\frac{1}{2}$x+1,
故答案为:ex-$\frac{1}{2}$x+1
点评 本题考查了导数的运算,考查了函数解析式的求法,解答此题的关键是明白原函数解析式中的f′(0)是常数,是基础题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
13.求曲线y=x2与y2=x所围成封闭图形的面积,其中正确的是( )
| A. | S=${∫}_{0}^{1}$($\sqrt{x}$-x2)dx | B. | S=${∫}_{0}^{1}$(y2-$\sqrt{x}$)dx | C. | S=${∫}_{0}^{1}$(x2-$\sqrt{x}$)dx | D. | S=${∫}_{0}^{2}$($\sqrt{y}$-y2)dy |
10.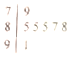 在华中师大一附中首届数学节的演讲比赛中,七位评委为某参赛教师打出的分数的茎叶图如图所示,去掉最高分和最低分后,这位老师得分的方差为( )
在华中师大一附中首届数学节的演讲比赛中,七位评委为某参赛教师打出的分数的茎叶图如图所示,去掉最高分和最低分后,这位老师得分的方差为( )
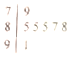 在华中师大一附中首届数学节的演讲比赛中,七位评委为某参赛教师打出的分数的茎叶图如图所示,去掉最高分和最低分后,这位老师得分的方差为( )
在华中师大一附中首届数学节的演讲比赛中,七位评委为某参赛教师打出的分数的茎叶图如图所示,去掉最高分和最低分后,这位老师得分的方差为( )| A. | 1.14 | B. | 1.6 | C. | 2.56 | D. | 3 |
11.若f(x)=f′(1)x2+ex,则f(1)=( )
| A. | e | B. | 0 | C. | e+1 | D. | e-1 |