题目内容
7.某学习小组、男女生共8人,现从男生中选2人,从女生中选1人,分别去做3种不同的工作,共有90种不同的选法,则男、女生人数为( )| A. | 男2人,女6人 | B. | 男3人,女5人 | C. | 男5人,女3人 | D. | 男6人,女2人 |
分析 设出男学生有x人,根据一共有8人得到女学生有8-x人,根据从男生中选2人,从女生中选1人分别去做3中不同的工作,共有90种不同的选法,得到关于x的等式Cx2C8-x1A33=90,解出x即可.
解答 解:设男学生有x人,则女学生有8-x人,
从男生中选2人,从女生中选1人分别去做3中不同的工作,共有90种不同的选法
∴Cx2C8-x1A33=90,
∴x(x-1)(8-x)=30=2×3×5,
∴x=3,8-3=5.
故选:B.
点评 本题考查排列、组合的综合运用,注意由x(x-1)(8-x)=30解出x的值运算量与难度都比较大,此时可以验证选项,进而选出答案.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
2.若函数f(x)在R上可导,且满足f(x)<x f′(x),则( )
| A. | 2 f(1)<f(2) | B. | 2 f(1)>f(2) | C. | 2 f(1)=f(2) | D. | f(1)=f(2) |
12.为了得到函数$y=2sin({\frac{x}{3}+\frac{π}{4}})$,x∈R的图象,只需把函数y=2sinx,x∈R的图象上所有的点( )
| A. | 向左平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{3}$倍 (纵坐标不变) | |
| B. | 向右平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标缩短到原来的$\frac{1}{3}$倍(纵坐标不变) | |
| C. | 向左平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) | |
| D. | 向右平移$\frac{π}{4}$个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) |
19.已知不等式(m2+4m-5)x2-4(m-1)x+3>0对一切实数x恒成立,则实数m的取值范围为( )
| A. | (-∞,-5)∪(1,+∞) | B. | (1,19) | C. | [1,19) | D. | (19,+∞) |
17.已知cosα=-$\frac{3}{5}$,α是第三象限的角,则sinα=( )
| A. | -$\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{4}{5}$ | D. | $\frac{4}{3}$ |
 是等差数列,
是等差数列, 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且 ,
, ,
, .
.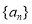 ,
, 的通项公式;
的通项公式; 的前
的前 项和
项和 .
. 的解组成的集合是 ( )
的解组成的集合是 ( )


